
 某校数学兴趣小组在探究如何求tan 15°,cos15°的值,经过自主思考、合作交流讨论,得到以下思路:
某校数学兴趣小组在探究如何求tan 15°,cos15°的值,经过自主思考、合作交流讨论,得到以下思路:分析 (1)根据思路二直接套用公式计算即可;
(2)作DE⊥AB于点E,CF⊥DE于点F,可得矩形BCFE,进而可得∠ODE=15°、∠DOE=75°,在RT△CDF中根据三角函数分别求出DF、CF=BE的长,在RT△ODE中求出DE的长,由BC=EF=DE-DF可得答案.
解答 解:(1)tan75°=tan(45°+30°)=$\frac{tan45°+tan30°}{1-tan45°•tan30°}$=$\frac{1+\frac{\sqrt{3}}{3}}{1-\frac{\sqrt{3}}{3}}$=2+$\sqrt{3}$;
cos15°=cos(60°-45°)=cos60°cos45°+sin60°sin45°=$\frac{1}{2}$×$\frac{\sqrt{2}}{2}$+$\frac{\sqrt{3}}{2}$×$\frac{\sqrt{2}}{2}$=$\frac{\sqrt{6}+\sqrt{2}}{4}$;
(2)如图2,作DE⊥AB于点E,CF⊥DE于点F,
∵BC⊥AB,
∴∠ABC=∠BEF=∠FEC=90°,
∴四边形BEFC是矩形,
∴∠FCB=90°,BC=EF,BE=CF,
∵DO⊥CD,
∴∠ODC=90°,
∴∠DOE+∠DOE=∠ODE+∠CDF=∠CDF+∠DCF=90°,
∴∠ODE=∠DCF=∠DCB-∠FCB=105°-90°=15°,
∠DOE=∠CDF=90°-15°=75°,
∵cos15°=$\frac{\sqrt{6}+\sqrt{2}}{4}$≈0.966,tan75°=2+$\sqrt{3}$≈3.732,
在RT△CDF中,CD=2米,
∴CF=DC•cos15°≈2×0.966=1.932米,
∵OE=OB-BE=0B-CF=5-1.932=3.068米,
∴DE=OE•tan75°=3.068×3.732=11.450米,
DF=CFtan75°=0.573,
∴BC=EF=DE-DF=11.450-0.573≈11(米),
答:此时路灯的灯柱BC的高度大约11米.
点评 本题考查了相似三角形的性质,直角三角形的性质,锐角三角函数的概念,正确的作出辅助线构造相似三角形是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
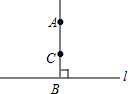 如图所示,因为AB⊥l,BC⊥l,B为垂足,所以AB和BC重合,其理由是( )
如图所示,因为AB⊥l,BC⊥l,B为垂足,所以AB和BC重合,其理由是( )| A. | 两点确定一条直线 | |
| B. | 在同一平面内,过一点有且只有一条直线与已知直线垂直 | |
| C. | 过一点能作一条垂线 | |
| D. | 垂线段最短 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{3}{2}$ | D. | $-\frac{3}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 7 | B. | 4 | C. | ±$\sqrt{3}$ | D. | ±3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com