
分析 (1)设方程另一根为x1,根据根与系数的关系可得出1+x1=m、1×x1=-2,由此可得出x1与m的值,此题得解;
(2)根据方程的系数结合根的判别式即可得出△=m2+8>0,由此得出方程有两个不相等的实数根.
解答 解:(1)设方程另一根为x1,
∵原方程为:x2-mx-2=0,
∴1+x1=m,1×x1=-2,
∴x1=-2,m=-1.
∴m的值为-1;方程的另一根为-2.
(2)对于任意的实数m,方程①总有两个不相等的实数根,理由如下:
∵在方程x2-mx-2=0中,△=(-m)2-4×1×(-2)=m2+8>0,
∴原方程有两个不相等的实数根.
点评 本题考查了根与系数的关系以及根的判别式,熟练掌握“两根之和为-$\frac{b}{a}$,两根之积为$\frac{c}{a}$”是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
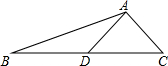 如图,AD是△ABC的中线,tanB=$\frac{1}{4}$,cosC=$\frac{\sqrt{2}}{2}$,AC=$\sqrt{2}$.
如图,AD是△ABC的中线,tanB=$\frac{1}{4}$,cosC=$\frac{\sqrt{2}}{2}$,AC=$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
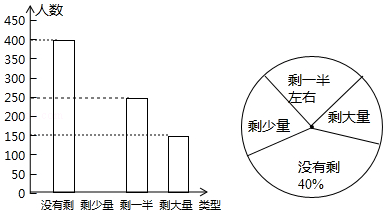
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com