
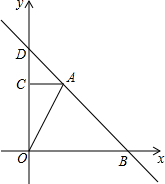 злКЯгыЬНОПЃКШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌRtЁїAOCЕФжБНЧБпOCдкyжсе§АыжсЩЯЃЌЧвЖЅЕуOгызјБъдЕужиКЯЃЌЕуAЕФзјБъЮЊЃЈ2ЃЌ4ЃЉЃЌжБЯпy=-x+bЙ§ЕуAЃЌгыxжсНЛгкЕуBЃЎ
злКЯгыЬНОПЃКШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌRtЁїAOCЕФжБНЧБпOCдкyжсе§АыжсЩЯЃЌЧвЖЅЕуOгызјБъдЕужиКЯЃЌЕуAЕФзјБъЮЊЃЈ2ЃЌ4ЃЉЃЌжБЯпy=-x+bЙ§ЕуAЃЌгыxжсНЛгкЕуBЃЎЗжЮі ЃЈ1ЃЉЯШНЋЕуAЃЈ2ЃЌ4ЃЉДњШыy=-x+bЃЌдЫгУД§ЖЈЯЕЪ§ЗЈЧѓГіжБЯпABЕФНтЮіЪНЃЌдйСюy=0ЃЌЧѓГіxЕФжЕЃЌМДПЩЕУЕНгыxжсНЛЕуBЕФзјБъЃЛ
ЃЈ2ЃЉЂйЯШЧѓГіжБЯпABгыyжсНЛЕуDЕФзјБъЃЌгЩBЁЂDСНЕуЕФзјБъЃЌПЩжЊЁїOBDЪЧЕШбќжБНЧШ§НЧаЮЃЌдйЙ§ЕуAзїANЁЭOBгкNЃЌПЩЕУAN=OC=4ЃЌBN=AN=4ЃЌдђЕБЕуPЕНДяЕуCЪБЃЌЕуMЕНДяЕуNЃЌЫљвдЗжСНжжЧщПіЬжТлЃКЃЈiЃЉЕБ0ЁмtЁм4ЃЌМДЕуPдкOCЩЯЃЌЕуQдкBAЩЯЪБЃЌгУКЌtЕФДњЪ§ЪНЗжБ№БэЪОPQЁЂCPЃЌдйИљОнS=$\frac{1}{2}$PQ•CPМДПЩЧѓНтЃЛЃЈiiЃЉЕБ4ЃМtЁм6ЃЌМДЕуPдкACЩЯЃЌЕуQдкAOЩЯЪБЃЌбгГЄMQНЛACгкЕуEЃЌгУКЌtЕФДњЪ§ЪНЗжБ№БэЪОAPЁЂQEЃЌдйИљОнS=$\frac{1}{2}$AP•QEМДПЩЧѓНтЃЛ
ЂкЗжСНжжЧщПіЬжТлЃКЃЈiЃЉЕБ0ЁмtЁм4ЃЌМДЕуPдкOCЩЯЃЌЕуQдкBAЩЯЪБЃЌЯШгЩШ§НЧаЮУцЛ§ЙЋЪНЧѓГіSЁїMPQ=-$\frac{1}{2}$t2+3tЃЌдйИљОнSЁїMPQ=S=$\frac{1}{2}$t2-5t+12СаГіЗНГЬЃЌНтЗНГЬМДПЩЃЛЃЈiiЃЉЕБ4ЃМtЁм6ЃЌМДЕуPдкACЩЯЃЌЕуQдкAOЩЯЪБЃЌЯШгЩШ§НЧаЮУцЛ§ЙЋЪНЧѓГіSЁїMPQ=ЃЈ6-tЃЉ|10-2t|ЃЌдйИљОнSЁїMPQ=S=ЃЈ6-tЃЉЃЈt-4ЃЉЃЌСаГіЗНГЬЃЌНтЗНГЬМДПЩЃЎ
НтД№ НтЃКЃЈ1ЃЉНЋЕуAЃЈ2ЃЌ4ЃЉДњШыy=-x+bЃЌ
ЕУ4=-2+bЃЌНтЕУb=6ЃЌ
ЁржБЯпABЕФНтЮіЪНЮЊЃКy=-x+6ЃЌ
ЕБy=0ЪБЃЌx=6ЃЌ
ЁрЕуBЕФзјБъЮЊЃЈ6ЃЌ0ЃЉЃЎ
ЃЈ2ЃЉЩшжБЯпy=-x+6гыyжсНЛгкЕуDЃЌдђDЃЈ0ЃЌ6ЃЉЃЌ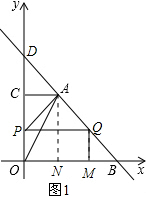 ЁпBЃЈ6ЃЌ0ЃЉЃЌ
ЁпBЃЈ6ЃЌ0ЃЉЃЌ
ЁрOB=OD=6ЃЌЁЯOBD=ЁЯODB=45ЁуЃЎ
Й§ЕуAЃЈ2ЃЌ4ЃЉзїANЁЭOBгкNЃЌдђAN=OC=4ЃЌON=AC=2ЃЌBN=AN=4ЃЌ
ЁрЕБЕуPЕНДяЕуCЪБЃЌЕуMЕНДяЕуNЃЎ
ЗжСНжжЧщПіЬжТлЃК
ЃЈiЃЉЕБ0ЁмtЁм4ЪБЃЌЕуPдкOCЩЯЃЌЕуQдкBAЩЯЃЌШчЭМ1ЃЎ
ЁпOP=tЃЌBM=QM=tЃЌ
ЁрPQЁЮOBЃЌPQ=OM=OB-BM=6-tЃЌCP=OC-OP=4-tЃЌ
ЁрS=$\frac{1}{2}$PQ•CP=$\frac{1}{2}$ЃЈ6-tЃЉЃЈ4-tЃЉ=$\frac{1}{2}$t2-5t+12ЃЛ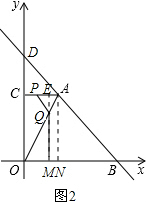 ЃЈiiЃЉЕБ4ЃМtЁм6ЪБЃЌЕуPдкACЩЯЃЌЕуQдкAOЩЯЃЌШчЭМ2ЃЌбгГЄMQНЛACгкЕуEЃЎ
ЃЈiiЃЉЕБ4ЃМtЁм6ЪБЃЌЕуPдкACЩЯЃЌЕуQдкAOЩЯЃЌШчЭМ2ЃЌбгГЄMQНЛACгкЕуEЃЎ
ЁпOC+CP=tЃЌBM=tЃЌ
ЁрAP=6-tЃЌOM=OB-BM=6-tЃЎ
ЁпtanЁЯAON=$\frac{QM}{OM}$=$\frac{AN}{ON}$ЃЌ
Ёр$\frac{QM}{6-t}$=$\frac{4}{2}$ЃЌ
ЁрQM=12-2tЃЌ
ЁрQE=EM-QM=4-ЃЈ12-2tЃЉ=2t-8ЃЌ
ЁрS=$\frac{1}{2}$AP•QE=$\frac{1}{2}$ЃЈ6-tЃЉЃЈ2t-8ЃЉ=-t2+10t-24ЃЎ
злЩЯПЩжЊЃЌS=$\left\{\begin{array}{l}{{\frac{1}{2}t}^{2}-5t+12ЃЈ0ЁмtЁм4ЃЉ}\\{{-t}^{2}+10t-24ЃЈ4ЃМtЁм6ЃЉ}\end{array}\right.$ЃЛ ЂкДцдквдMЁЂPЁЂQЮЊЖЅЕуЕФШ§НЧаЮЕФУцЛ§гыSЯрЕШЃЌРэгЩШчЯТЃК
ЂкДцдквдMЁЂPЁЂQЮЊЖЅЕуЕФШ§НЧаЮЕФУцЛ§гыSЯрЕШЃЌРэгЩШчЯТЃК
ЗжСНжжЧщПіЬжТлЃК
ЃЈiЃЉЕБ0ЁмtЁм4ЪБЃЌЕуPдкOCЩЯЃЌЕуQдкBAЩЯЃЌШчЭМ3ЃЎ
ЁпSЁїMPQ=$\frac{1}{2}$PQ•QM=$\frac{1}{2}$ЃЈ6-tЃЉt=-$\frac{1}{2}$t2+3tЃЌS=$\frac{1}{2}$t2-5t+12ЃЌ
Ёр-$\frac{1}{2}$t2+3t=$\frac{1}{2}$t2-5t+12ЃЌ
ећРэЃЌЕУt2-8t+12=0ЃЌ
НтЕУt1=2ЃЌt2=6ЃЈВЛКЯЬтвтЩсШЅЃЉЃЛ
ЃЈiiЃЉЕБ4ЃМtЁм6ЪБЃЌЕуPдкACЩЯЃЌЕуQдкAOЩЯЃЌШчЭМ4ЃЎ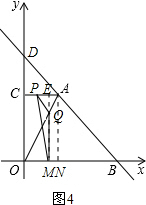 ЁпQM=12-2tЃЌPE=|CE-CP|=|ЃЈ6-tЃЉ-ЃЈt-4ЃЉ|=|10-2t|ЃЌ
ЁпQM=12-2tЃЌPE=|CE-CP|=|ЃЈ6-tЃЉ-ЃЈt-4ЃЉ|=|10-2t|ЃЌ
ЁрSЁїMPQ=$\frac{1}{2}$QM•PE=$\frac{1}{2}$ЃЈ12-2tЃЉ|10-2t|=ЃЈ6-tЃЉ|10-2t|ЃЌ
гжЁпS=$\frac{1}{2}$AP•QE=$\frac{1}{2}$ЃЈ6-tЃЉЃЈ2t-8ЃЉ=ЃЈ6-tЃЉЃЈt-4ЃЉЃЌ
ЁрЃЈ6-tЃЉ|10-2t|=ЃЈ6-tЃЉЃЈt-4ЃЉЃЌ
Ёпt=6ЪБЃЌMгыQжиКЯЃЌВЛКЯЬтвтЩсШЅЃЌ
Ёр10-2t=ЁРЃЈt-4ЃЉЃЌ
ЕБ10-2t=t-4ЪБЃЌt=$\frac{14}{3}$ЃЛ
ЕБ10-2t=-ЃЈt-4ЃЉЪБЃЌt=6ЩсШЅЃЎ
злЩЯПЩжЊЃЌДцдквдMЁЂPЁЂQЮЊЖЅЕуЕФШ§НЧаЮЕФУцЛ§гыSЯрЕШЃЌДЫЪБtЕФжЕЮЊ2Лђ$\frac{14}{3}$ЃЎ
ЕуЦР БОЬтЪЧвЛДЮКЏЪ§ЕФзлКЯЬтаЭЃЌжївЊПМВщСЫдЫгУД§ЖЈЯЕЪ§ЗЈЧѓжБЯпЕФНтЮіЪНЃЌЕШбќжБНЧШ§НЧаЮЕФаджЪЃЌШ§НЧКЏЪ§ЕФЖЈвхЃЌШ§НЧаЮЕФУцЛ§ЃЌвЊзЂвтЃЈ2ЃЉжаЃЌвЊИљОнPгыQЕуЕФВЛЭЌЮЛжУНјааЗжРрЧѓНтЃЌБОЬтФбЖШЪЪжаЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | ШёНЧШ§НЧаЮ | BЃЎ | жБНЧШ§НЧаЮ | CЃЎ | ЖлНЧШ§НЧаЮ | DЃЎ | ЕШбќШ§НЧаЮ |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
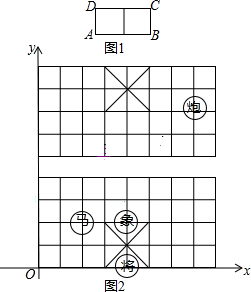 жаЙњЯѓЦхжаРњРДгаЁАТэЁБзпЁАШеЁБЃЌЁАЯѓЁБЗЩЁАЬяЁБжЎЫЕЃЌЦфвтЫМЪЧЃКдкЯѓЦхЦхХЬЩЯЃЌЁАТэЁБЕФзпЗЈШчЯТЃКвдЁАТэЁБЫљдкЕФЮЛжУЮЊЦхИёЫљзщГЩЕФШЮвЛЁАШеЁБзжЕФвЛИіЖЅЕуЃЌЯТвЛВНЁАТэЁБПЩвдзпЕНИУЁАШеЁБзжгыдЮЛжУЯрЖдЕФФЧИіЖЅЕуЃЌШчЭМ1ТэПЩвдздAзпЕНCЃЈЛђздCзпЕНAЃЉвВПЩздBзпЕНDЃЈЛђDзпЕНBЃЉЃЌдкШчЭМЦхХЬжаЃЌНЈСЂШчЭМ2ЫљЪОжБНЧзјБъЯЕЃК
жаЙњЯѓЦхжаРњРДгаЁАТэЁБзпЁАШеЁБЃЌЁАЯѓЁБЗЩЁАЬяЁБжЎЫЕЃЌЦфвтЫМЪЧЃКдкЯѓЦхЦхХЬЩЯЃЌЁАТэЁБЕФзпЗЈШчЯТЃКвдЁАТэЁБЫљдкЕФЮЛжУЮЊЦхИёЫљзщГЩЕФШЮвЛЁАШеЁБзжЕФвЛИіЖЅЕуЃЌЯТвЛВНЁАТэЁБПЩвдзпЕНИУЁАШеЁБзжгыдЮЛжУЯрЖдЕФФЧИіЖЅЕуЃЌШчЭМ1ТэПЩвдздAзпЕНCЃЈЛђздCзпЕНAЃЉвВПЩздBзпЕНDЃЈЛђDзпЕНBЃЉЃЌдкШчЭМЦхХЬжаЃЌНЈСЂШчЭМ2ЫљЪОжБНЧзјБъЯЕЃКВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
 ШчЭМЃЌвЛЫвТжДЌЮЛгкЕЦЫўBЕФе§ЮїЗНЯђAДІЃЌЧвAДІгыЕЦЫўBЯрОр60КЃРяЃЌТжДЌбиЖЋББЗНЯђдШЫйЧАааЃЌЕНДяЮЛгкЕЦЫўBЕФББЦЋЖЋ15ЁуЗНЯђЩЯЕФCДІЃЎ
ШчЭМЃЌвЛЫвТжДЌЮЛгкЕЦЫўBЕФе§ЮїЗНЯђAДІЃЌЧвAДІгыЕЦЫўBЯрОр60КЃРяЃЌТжДЌбиЖЋББЗНЯђдШЫйЧАааЃЌЕНДяЮЛгкЕЦЫўBЕФББЦЋЖЋ15ЁуЗНЯђЩЯЕФCДІЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | ЯђзѓЦНвЦ2ИіЕЅЮЛЃЌдйЯђЯТЦНвЦ2ИіЕЅЮЛ | |
| BЃЎ | ЯђгвЦНвЦ2ИіЕЅЮЛЃЌдйЯђЩЯЦНвЦ2ИіЕЅЮЛ | |
| CЃЎ | ЯђзѓЦНвЦ1ИіЕЅЮЛЃЌдйЯђЩЯЦНвЦ1ИіЕЅЮЛ | |
| DЃЎ | ЯђгвЦНвЦ1ИіЕЅЮЛЃЌдйЯђЯТЦНвЦ1ИіЕЅЮЛ |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com