
【题目】随着科学技术的不断进步,我国海上能源开发和利用已达到国际领先水平.下图为我国在南海海域自主研制的海上能源开发的机器装置AB,一直升飞机在离海平面l距离为150米的空中点P处,看到该机器顶部点A处的俯角为38°,看到露出海平面的机器部分点B处的俯角为65°,求这个机器装置露出海平面部分AB的高度?(结果精确到0.1,参考数据:sin65°=0.9063,sin38°=0.6157,tan38°=0.7813,tan65°=2.1445.)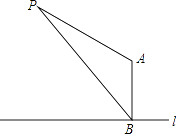
【答案】解:依题意 PC⊥BC PD⊥l 垂足分别为点C、D,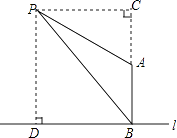
∠CPA=38°,∠CPB=∠PBD=65°,
∵ ![]()
∴DB= ![]() =69.9464,
=69.9464,
又∵tan∠CPA= ![]() ,DB=PC,
,DB=PC,
∴AC=PCtan38°=69.9464×0.7813=54.6491,
∴AB=CB﹣CA=150﹣54.6491≈95.4(米).
答:这个机器装置露出海平面的高度约是95.4米.
【解析】根据仰角、俯角的定义,过P作AB、l的垂线,构造直角三角形,用解直角三角形的知识来解决.
【考点精析】关于本题考查的解直角三角形,需要了解解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】列一元一次方程解应用题:
某管道由甲、乙两工程队单独施工分别需要30天、20天.
(1)如果两队从管道两端同时施工,需要多少天完工?
(2)又知甲队单独施工每天需付200元施工费,乙队单独施工每天需付280元施工费,那么是由甲队单独施工,还是由乙队单独施工,还是由两队同时施工?请你按照少花钱多办事的原则,设计一个方案,并通过计算说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式:
第一个等式:a1=![]()
第二个等式:a2=![]()
第三个等式:a3=![]()
……
按以上规律解答下列问题:
(1)列出第五个等式:a5=
(2)计算a1+a2+a3+a4+a5的结果.
(3)计算a1+a2+a3+……+an﹣1+an的结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的AC边在直线m上,∠ACB=80°,以C为圆心, ![]() BC长为半径画弧,交直线m于点D1、交BC于点E1 , 连接D1E1;又以D1为圆心,
BC长为半径画弧,交直线m于点D1、交BC于点E1 , 连接D1E1;又以D1为圆心, ![]() D1E1长为半径画弧,交直线m于点D2、交D1E1于点E2 , 连接D2E2;又以D2为圆心,
D1E1长为半径画弧,交直线m于点D2、交D1E1于点E2 , 连接D2E2;又以D2为圆心, ![]() D2E2长为半径画弧,交直线m于点D3、交D2E2于点E3 , 连接D3E3;如此依次下去,…,第n次时所得的∠EnDnDn﹣1= .
D2E2长为半径画弧,交直线m于点D3、交D2E2于点E3 , 连接D3E3;如此依次下去,…,第n次时所得的∠EnDnDn﹣1= . 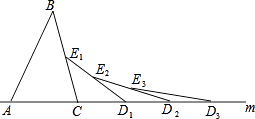
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的三个顶点都在格点上,每个小方格边长均为1个单位长度,建立如图坐标系.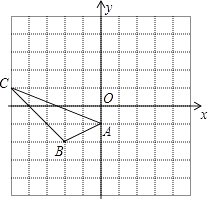
(1)请你作出△ABC关于点A成中心对称的△AB1C1(其中B的对称点是B1 , C的对称点是C1),并写出点B1、C1的坐标.
(2)依次连接BC1、C1B1、B1C.猜想四边形BC1B1C是什么特殊四边形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD>AB,将矩形ABCD折叠,使点C与点A重合,折痕为MN,连接CN.若△CDN的面积与△CMN的面积比为1:4,则 ![]() 的值为( )
的值为( ) 
A.2
B.4
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),公路上有A、B、C三个车站,一辆汽车从A站以速度v1匀速驶向B站,到达B站后不停留,以速度v2匀速驶向C站,汽车行驶路程y(千米)与行驶时间x(小时)之间的函数图象如图(2)所示.
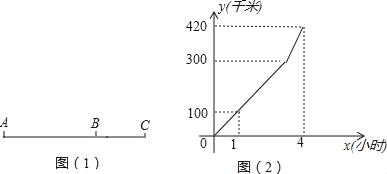
(1)当汽车在A、B两站之间匀速行驶时,求y与x之间的函数关系式及自变量的取值范围;
(2)求出v2的值;
(3)若汽车在某一段路程内刚好用50分钟行驶了90千米,求这段路程开始时x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是初三某班女生的体重检查结果:
体重(kg) | 34 | 35 | 38 | 40 | 42 | 45 | 50 |
人数 | 1 | 2 | 5 | 5 | 4 | 2 | 1 |
根据表中信息,回答下列问题:
(1)该班女生体重的中位数是;
(2)该班女生的平均体重是kg;
(3)根据上表中的数据补全条形统计图. 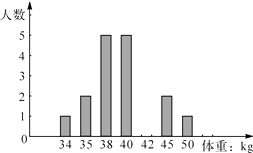
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校有1500名学生参加首届“我爱我们的课堂”为主题的图片制作比赛,赛后随机抽取部分参赛学生的成绩进行整理并制作成图表如图:
分数段 | 频数 | 频率 |
60≤x<70 | 40 | 0.40 |
70≤x<80 | 35 | b |
80≤x<90 | a | 0.15 |
90≤x<100 | 10 | 0.10 |
频率分布统计表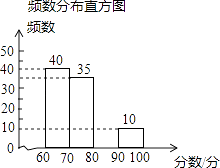
请根据上述信息,解答下列问题:
(1)分别求出a、b的值;
(2)请补全频数分布直方图;
(3)如果将比赛成绩80分以上(含80分)定为优秀,那么优秀率是多少?并且估算该校参赛学生获得优秀的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com