
分析 (1)当0≤x≤10时,每人单价为1200元;当10<x≤30时,根据每人单价=原定每人单价-因人数增减而减少的价格,可列函数关系;
(2)根据营业额=每人单价×人数,分别列出0≤x≤10、10<x≤30的函数关系式,求出相应范围内的最值,比较可得.
解答 解:(1)当0≤x≤10时,y=1200;
当10<x≤30时,y=1200-20(x-10)=-20x+1400;
故y与x间的函数关系式为:y=$\left\{\begin{array}{l}{1200}&{0≤x≤10}\\{-20x+1400}&{10<x≤30}\end{array}\right.$.
(2)设旅行社可以获的营业额为W元,
当0≤x≤10时,W=1200x;
∵W随x的增大而增大,
∴当x=10时,W取得最大值,最大值为12000元;
当10<x≤30时,W=(-20x+1400)x=-20x2+1400x=-20(x-35)2+24500,
∵x<35时,W随x的增大而增大,
∴当x=30时,W取得最大值,最大值为W=-20(30-35)2+24500=24000元,
综上,当x=30时,W取得最大值24000元.
答:当考察团人数为30人时,该旅行社可以获得最大营业额,最大营业额是24000元.
点评 本题考查了二次函数的应用,解答本题的关键是仔细审题建立函数关系式,利用函数知识解决实际问题,注意掌握配方法求最值的应用.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
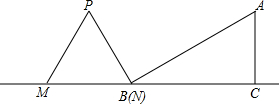
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com