
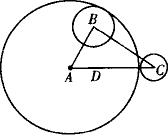
如图,⊙A与⊙B内切,⊙A与⊙C外切,⊙A,⊙B,⊙C的半径分别为2![]() +
+![]() ,
,![]() ,2
,2![]() -
-![]() ,∠BAC=60°,求BC长.
,∠BAC=60°,求BC长.
|
解析:过B点作BD⊥AC于D. ∵⊙A与⊙B内切, ⊙A与⊙C外切,且⊙A,⊙B,⊙C的半径分别为2 ∴AB=rA-rB=2 AC=rA+rC=2 ∵∠BAC=60°, ∴AD=AB·cos∠BAC=AB·cos60°, ∴AD=2 ∴BD=AB·sin∠BAC=AB·sin60°. ∴BD=2 ∴DC=AC-AD=3 ∵BC2=BD2+DC2, ∴BC2=(3 或由BD=DC,得∠C=45°,∴BC=
思路点拨:当两圆相切时,有两圆圆心与切点共线.因此,当两圆内切时,圆心距为两圆半径之差;当两圆外切时,两圆圆心距为两圆半径之和.因此,AB=rA-rB,AC=rA+rC.但注意,△ABC不一定是Rt△,利用特殊角∠BAC=60°,过B点作高BD,构造两个直角三角形,进而利用勾股定理求得BC长. 评注:两圆相切时,要注意说明两圆心与切点三点共线,设法构成直角三角形利用勾股定理解题. |


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
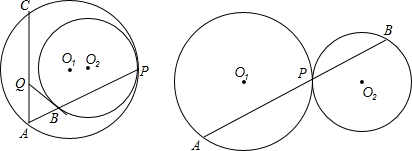
 垂直于OC,垂足为点E.
垂直于OC,垂足为点E.| 5 |
| ||
| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
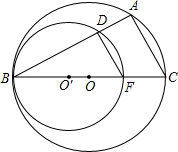 ⊙O的弦BA交⊙O′于点D,连接DF、AC、CD.
⊙O的弦BA交⊙O′于点D,连接DF、AC、CD.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
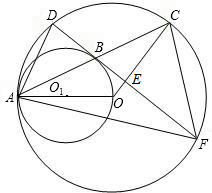
 (1997•武汉)如图,⊙O1与⊙O内切于点A,△ABC内接于⊙O,AB、AC分别交⊙O1于点E和F,BD切⊙O1于点D,且FD是⊙O1的直径,延长FE交BD于点H.
(1997•武汉)如图,⊙O1与⊙O内切于点A,△ABC内接于⊙O,AB、AC分别交⊙O1于点E和F,BD切⊙O1于点D,且FD是⊙O1的直径,延长FE交BD于点H.| DH |
| HB |
| 4 |
| 5 |
| AE |
| AB |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com