
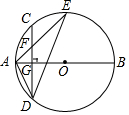
 如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足$\frac{CF}{FD}$=$\frac{1}{3}$,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3.给出下列结论:
如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足$\frac{CF}{FD}$=$\frac{1}{3}$,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3.给出下列结论:| A. | ①②③ | B. | ①②④ | C. | ②③④ | D. | ②④ |
分析 ①由三角形的外角大于与它不相邻的任何一个内角得出∠DFE>DAF,
②由AB是⊙O的直径,弦CD⊥AB,根据垂径定理可得:$\widehat{AD}=\widehat{AC}$,DG=CG,继而证得△ADF∽△AED;
③由勾股定理可求得AG的长,即可求得tan∠ADF的值,继而求得tan∠E=$\frac{\sqrt{5}}{4}$;
④首先求得△ADF的面积,由相似三角形面积的比等于相似比,即可求得△ADE的面积,继而求得S△DEF=4 $\sqrt{5}$
解答 解:根据三角形的外角的性质得:∠DFE>DAF,
∴△ADF与△FED不可能相似,
故①错误;
②∵AB是⊙O的直径,弦CD⊥AB,
∴$\widehat{AD}=\widehat{AC}$,DG=CG,
∴∠ADF=∠AED,
∵∠FAD=∠DAE(公共角),
∴△ADF∽△AED;
∴$\frac{AD}{AE}=\frac{AF}{AD}$,
∴AD2=AF•AE
故②正确;
③∵AF=3,FG=2,
∴AG=$\sqrt{A{F}^{2}-F{G}^{2}}$=$\sqrt{5}$,
∴在Rt△AGD中,tan∠ADG=$\frac{AG}{DG}=\frac{\sqrt{5}}{4}$,
∴tan∠E=$\frac{\sqrt{5}}{4}$;
故③错误;
④∵DF=DG+FG=6,AD=$\sqrt{A{G}^{2}+D{G}^{2}}$=$\sqrt{21}$,
∴S△ADF=$\frac{1}{2}$DF•AG=$\frac{1}{2}$×6×$\sqrt{5}$=3 $\sqrt{5}$,
∵△ADF∽△AED,
∴$\frac{{S}_{△ADF}}{{S}_{△AED}}$=( $\frac{AF}{AD}$)2,
∴$\frac{3\sqrt{5}}{{S}_{△AED}}=\frac{3}{7}$,
∴S△AED=7 $\sqrt{5}$,
∴S△DEF=S△AED-S△ADF=4 $\sqrt{5}$;
故④正确.
故选D.
点评 此题考查了相似三角形的判定与性质、圆周角定理、垂径定理、勾股定理以及三角函数等知识.此题综合性较强,难度适中,注意掌握数形结合思想的应用


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:选择题
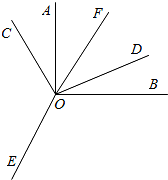 如图,平面内∠AOB=∠COD=90°,∠COE=∠BOE,OF平分∠AOD,则以下结论:
如图,平面内∠AOB=∠COD=90°,∠COE=∠BOE,OF平分∠AOD,则以下结论:| A. | ①②④ | B. | ①②③ | C. | ①③④ | D. | ②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
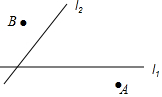 现有两条高速公路l1、l2和两个城镇A、B(如图),准备建一个燃气控制中心站P,使中心站到两条公路距离相等,并且到两个城镇的距离也相等,请你利用直尺和圆规作出中心站P的位置.
现有两条高速公路l1、l2和两个城镇A、B(如图),准备建一个燃气控制中心站P,使中心站到两条公路距离相等,并且到两个城镇的距离也相等,请你利用直尺和圆规作出中心站P的位置.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 垂直于半径的直线一定是这个圆的切线 | |
| B. | 在同圆中,同弦或等弦所对的圆周角相等 | |
| C. | 三角形有且只有一个内切圆 | |
| D. | 三角形的内心到三角形的3个顶点的距离相等 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 72° | B. | 72°或144° | C. | 144° | D. | 144°或216° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
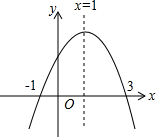 如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:①2a+b=0;②a+b+c>0;③当-1<x<3时,y>0;④-a+c<0.其中正确的个数为( )
如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:①2a+b=0;②a+b+c>0;③当-1<x<3时,y>0;④-a+c<0.其中正确的个数为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com