
【题目】对于平面直角坐标系![]() 中的点
中的点![]() 和
和![]() ,给出如下定义:连接
,给出如下定义:连接![]() 交
交![]() 于点
于点![]() ,若点
,若点![]() 关于点
关于点![]() 的对称点
的对称点![]() 在
在![]() 的内部,则称点
的内部,则称点![]() 是
是![]() 的外称点.
的外称点.

(1)当![]() 的半径为
的半径为![]() 时,
时,
①在点![]() 中,
中,![]() 的外称点是 ;
的外称点是 ;
②若点![]() 为
为![]() 的外称点,且线段
的外称点,且线段![]() 交
交![]() 于点
于点 ,求
,求![]() 的取值范围;
的取值范围;
(2)直线![]() 过点
过点![]() , 与
, 与![]() 轴交于点
轴交于点![]() .
. ![]() 的圆心为
的圆心为![]() , 半径为
, 半径为![]() 若线段
若线段![]() 上的所有点都是
上的所有点都是![]() 的外称点,请直接写出
的外称点,请直接写出![]() 的取值范围.
的取值范围.
【答案】(1)① ![]() ;②
;② ![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】
(1) ①由外称点的定义可知:![]() 到圆心的距离小于3且大于1,点
到圆心的距离小于3且大于1,点![]() 才是
才是![]() 的外称点,据此可求得答案;②由点
的外称点,据此可求得答案;②由点 知,点G在一、三象限角平分线上,则点
知,点G在一、三象限角平分线上,则点![]() 也在一、三象限角平分线上,根据外称点的定义,
也在一、三象限角平分线上,根据外称点的定义,![]() ,且
,且![]() ,由两点之间的距离公式可求得
,由两点之间的距离公式可求得![]() 的取值范围;
的取值范围;
(2)根据外称点的定义,分点![]() 在点B左侧时和右侧两种情况,线段
在点B左侧时和右侧两种情况,线段![]() 上的点离
上的点离![]() 最远的点要小于3,离
最远的点要小于3,离![]() 最近的点要大于1,画出图形,利用数形结合思想,即可解答.
最近的点要大于1,画出图形,利用数形结合思想,即可解答.
(1) ①由外称点的定义可知:![]() 到圆心的距离小于3且大于1,点
到圆心的距离小于3且大于1,点![]() 才是
才是![]() 的外称点,
的外称点,
点D(-1,-1),![]() , 点D是
, 点D是![]() 的外称点,
的外称点,
点E(2,0),![]() , 点E是
, 点E是![]() 的外称点,
的外称点,
点F(0,4),![]() , 点F不是
, 点F不是![]() 的外称点,
的外称点,
故答案是:![]()
②由点 知,点G在一、三象限角平分线上,则点
知,点G在一、三象限角平分线上,则点![]() 也在一、三象限角平分线上,
也在一、三象限角平分线上,
∴![]() ,
,![]()
由外称点的定义可知:![]() ,即
,即![]() ,解得:
,解得:![]()
又![]() ,则
,则![]()
∴![]() 的取值范围是:
的取值范围是:![]() .
.
(2) ∵直线![]() 过点
过点![]() ,代入求得:
,代入求得:![]() ,
,
∴直线的解析式是:![]() ,则与
,则与![]() 轴交于点
轴交于点![]() 的坐标是(2,0),与y轴交于点C的坐标是(0,2),∴
的坐标是(2,0),与y轴交于点C的坐标是(0,2),∴![]() 为等腰直角三角形,
为等腰直角三角形,
当点![]() 在点B左侧时,如图1,离
在点B左侧时,如图1,离![]() 最远的点为点B,依题意:
最远的点为点B,依题意:![]() ,∴
,∴![]() ,
,
当![]() 与线段
与线段![]() 相切时,切点离
相切时,切点离![]() 为最近,如图2:作
为最近,如图2:作![]() 于D,
于D,
∴![]() 为等腰直角三角形,
为等腰直角三角形,![]()
∴![]() ,则
,则![]() ,∴依题意:
,∴依题意:![]()
故当点![]() 在点B左侧时,
在点B左侧时,![]() ;
;


当点![]() 在点B右侧时,如图3,离
在点B右侧时,如图3,离![]() 最近的点为点B,依题意:
最近的点为点B,依题意:![]() ,∴
,∴![]() ,
,
离![]() 最远的点为点A,如图4,依题意:
最远的点为点A,如图4,依题意:![]() ,
,
由两点之间距离公式:![]() ,
,
解得:![]() (因为T在B右侧,
(因为T在B右侧,![]() 舍去)
舍去)
故当点![]() 在点B右侧时,
在点B右侧时,![]()
综上所述,答案是:![]() 或
或![]()




 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案科目:初中数学 来源: 题型:
【题目】如图,把![]() 置于平面直角坐标系中,点A的坐标为
置于平面直角坐标系中,点A的坐标为![]() ,点B的坐标为
,点B的坐标为![]() ,点P是
,点P是![]() 内切圆的圆心.将
内切圆的圆心.将![]() 沿x轴的正方向作无滑动滚动,使它的三边依次与x轴重合,第一次滚动后圆心为
沿x轴的正方向作无滑动滚动,使它的三边依次与x轴重合,第一次滚动后圆心为![]() ,第二次滚动后圆心为
,第二次滚动后圆心为![]() ,…,依此规律,第2019次滚动后,
,…,依此规律,第2019次滚动后,![]() 内切圆的圆心
内切圆的圆心![]() 的坐标是________.
的坐标是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,以点C(2,![]() )为圆心,以2为半径的圆与x轴交于A,B两点.
)为圆心,以2为半径的圆与x轴交于A,B两点.
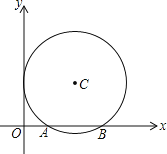
(1)求A,B两点的坐标;
(2)若二次函数y=x2+bx+c的图象经过点A,B,试确定此二次函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣2,与x轴的一个交点在(﹣3,0)和(﹣4,0)之间,其部分图象如图所示则下列结论:①4a﹣b=0;②c<0;③c>3a;④4a﹣2b>at2+bt(t为实数);⑤点(﹣![]() ,y1),(﹣
,y1),(﹣![]() ,y2),(
,y2),(![]() )是该抛物线上的点,则y2<y1<y3,其中,正确结论的个数是( )
)是该抛物线上的点,则y2<y1<y3,其中,正确结论的个数是( )

A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】运动员将小球沿与地面成一定角度的方向击出,在不考虑空气阻力的条件下,小球的飞行高度h(m)与它的飞行时间t(s)满足二次函数关系,t与h的几组对应值如下表所示.
t(s) | 0 | 0.5 | 1 | 1.5 | 2 | … |
h(m) | 0 | 8.75 | 15 | 18.75 | 20 | … |
(1)求h与t之间的函数关系式(不要求写t的取值范围);
(2)求小球飞行3s时的高度;
(3)问:小球的飞行高度能否达到22m?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】文艺复兴时期,意大利艺术大师达芬奇曾研究过圆弧所围成的许多图形的面积问题. 如图所示称为达芬奇的“猫眼”,可看成圆与正方形的各边均相切,切点分别为![]() ,
,![]() 所在圆的圆心为点
所在圆的圆心为点![]() (或
(或![]() ). 若正方形的边长为2,则图中阴影部分的面积为( )
). 若正方形的边长为2,则图中阴影部分的面积为( )

A. ![]() B. 2C.
B. 2C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣![]() (x﹣k)2+
(x﹣k)2+![]() 经过点D(﹣1,0),与x轴正半轴交于点E,与y轴交于点C,过点C作CB∥x轴交抛物线于点B.连接BD交y轴于点F.
经过点D(﹣1,0),与x轴正半轴交于点E,与y轴交于点C,过点C作CB∥x轴交抛物线于点B.连接BD交y轴于点F.
(1)求点E的坐标.
(2)求△CFB的面积.
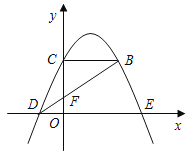
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y1=![]() (x+1)2+1与y2=a(x﹣4)2﹣3交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于B、C两点,且D、E分别为顶点.则下列结论:①a=
(x+1)2+1与y2=a(x﹣4)2﹣3交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于B、C两点,且D、E分别为顶点.则下列结论:①a=![]() ;②AC=AE;③△ABD是等腰直角三角形;④当x>1时,y1>y2 其中正确结论的个数是( )
;②AC=AE;③△ABD是等腰直角三角形;④当x>1时,y1>y2 其中正确结论的个数是( )
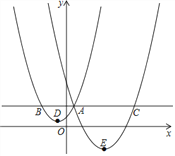
A. 1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com