
| A. | 13 | B. | $\frac{240}{13}$ | C. | 120 | D. | $\frac{120}{13}$ |
科目:初中数学 来源: 题型:解答题
 如图,BF为⊙O的直径,直线AC交⊙O于A,B两点,点D在⊙O上,BD平分∠OBC,DE⊥AC于点E.
如图,BF为⊙O的直径,直线AC交⊙O于A,B两点,点D在⊙O上,BD平分∠OBC,DE⊥AC于点E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
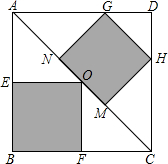 如图,正方形ABCD是一块绿化带,其中阴影部分EOFB、GHMN都是正方形的花圃,其中点N、O、M均在AC上,点G、H、F、E分别在AD、DC、CB、BA上,一只自由飞翔的小鸟,将随机落在这块绿化带上,则小鸟落在花圃上的概率为( )
如图,正方形ABCD是一块绿化带,其中阴影部分EOFB、GHMN都是正方形的花圃,其中点N、O、M均在AC上,点G、H、F、E分别在AD、DC、CB、BA上,一只自由飞翔的小鸟,将随机落在这块绿化带上,则小鸟落在花圃上的概率为( )| A. | $\frac{17}{32}$ | B. | $\frac{1}{2}$ | C. | $\frac{17}{36}$ | D. | $\frac{17}{38}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 为有效开发海洋资源,保护海洋权益,我国对南海诸岛进行了全面调查.如图,一测量船在A岛测得B岛在北偏西30°方向,C岛在北偏东15°方向,航行100海里到达B岛,在B岛测得C岛在北偏东45°,求B,C两岛及A,C两岛的距离.(结果保留到整数,$\sqrt{2}$≈1.41,$\sqrt{6}$≈2.45)
为有效开发海洋资源,保护海洋权益,我国对南海诸岛进行了全面调查.如图,一测量船在A岛测得B岛在北偏西30°方向,C岛在北偏东15°方向,航行100海里到达B岛,在B岛测得C岛在北偏东45°,求B,C两岛及A,C两岛的距离.(结果保留到整数,$\sqrt{2}$≈1.41,$\sqrt{6}$≈2.45)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
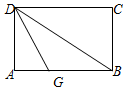 如图,将矩形纸片ABCD折叠,先折出折痕(对角线)BD,再折叠,使边DA与对角线BD重合,得折痕DG,若AB=8,BC=6,则AG的长是3.
如图,将矩形纸片ABCD折叠,先折出折痕(对角线)BD,再折叠,使边DA与对角线BD重合,得折痕DG,若AB=8,BC=6,则AG的长是3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com