
【题目】已知抛物线y=x2+bx+c经过点(1,0)和点(0,3).
(1)求此抛物线的解析式及顶点坐标;
(2)当自变量x满足﹣1≤x≤3时,求函数值y的取值范围;
(3)将此抛物线沿x轴平移m个单位后,当自变量x满足1≤x≤5时,y的最小值为5,求m的值.
【答案】(1) 抛物线解析式为y=x2﹣4x+3, 顶点坐标为(2,﹣1);(2) ﹣1≤x<8;(3) m的值为3+![]() 或1+
或1+![]()
【解析】
(1)利用待定系数法求抛物线解析式;然后把一般式配成顶点式得到抛物线的顶点坐标;
(2)先计算出当x=﹣1和x=3对应的函数值,然后根据二次函数的性质解决问题;
(3)设此抛物线沿x轴向右平移m个单位后抛物线解析式为y=(x﹣2﹣m)2﹣1,利用二次函数的性质,当2+m>5,此时x=5时,y=5,即(5﹣2﹣m)2﹣1=5,;设此抛物线沿x轴向左平移m个单位后抛物线解析式为y=(x﹣2+m)2﹣1,利用二次函数的性质得到2﹣m<1,此时x=1时,y=5,即(1﹣2﹣m)2﹣1=5,然后分别解关于m的方程即可.
解:(1)把(1,0),(0,3)代入y=x2+bx+c得![]() 解得
解得![]()
∴抛物线解析式为y=x2﹣4x+3;
∵y=x2﹣4x+3=(x﹣2)2﹣1,
∴抛物线的顶点坐标为(2,﹣1);
(2)当x=﹣1时,y=x2﹣4x+3=8,
当x=3时,y=x2﹣4x+3=0,
∴当﹣1≤x≤3时,函数值y的取值范围为﹣1≤x<8;
(3)设此抛物线沿x轴向右平移m个单位后抛物线解析式为y=(x﹣2﹣m)2﹣1,
∵当自变量x满足1≤x≤5时,y的最小值为5,
∴2+m>5,即m>3,
此时x=5时,y=5,即(5﹣2﹣m)2﹣1=5,解得m1=3+![]() ,m2=3﹣
,m2=3﹣![]() (舍去),
(舍去),
设此抛物线沿x轴向左平移m个单位后抛物线解析式为y=(x﹣2+m)2﹣1,
∵当自变量x满足1≤x≤5时,y的最小值为5,
∴2﹣m<1,即m>1,
此时x=1时,y=5,即(1﹣2﹣m)2﹣1=5,解得m1=1+![]() ,m2=1﹣
,m2=1﹣![]() (舍去),
(舍去),
综上所述,m的值为3+![]() 或1+
或1+![]() .
.


科目:初中数学 来源: 题型:
【题目】图1是一个地铁站入口的双翼闸机.如图2,它的双翼展开时,双翼边缘的端点A与B之间的距离为10cm,双翼的边缘AC=BD=54cm,且与闸机侧立面夹角∠PCA=∠BDQ=30°.当双翼收起时,可以通过闸机的物体的最大宽度为( )

A. (54![]() +10) cm B. (54
+10) cm B. (54![]() +10) cm C. 64 cm D. 54cm
+10) cm C. 64 cm D. 54cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,点O在BC边上,∠BAC的平分线交⊙O于点D,连接BD、CD,过点D作BC的平行线与AC的延长线相交于点P.
(1)求证:PD是⊙O的切线;
(2)求证:ABCP=BDCD;
(3)当AB=5cm,AC=12cm时,求线段PC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,往竖直放置的在A处由短软管连接的粗细均匀细管组成的“U”形装置中注入一定量的水,水面高度为6cm,现将右边细管绕A处顺时针旋转60°到AB位置,且左边细管位置不变,则此时“U”形装置左边细管内水柱的高度约为( )
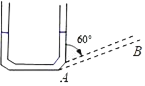
A. 4cmB. 2![]() cmC. 3cmD. 8cm
cmC. 3cmD. 8cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】东东玩具商店用500元购进一批悠悠球,很受中小学生欢迎,悠悠球很快售完,接着又用900元购进第二批这种悠悠球,所购数量是第一批数量的1.5倍,但每套进价多了5元.
(1)求第一批悠悠球每套的进价是多少元;
(2)如果这两批悠悠球每套售价相同,且全部售完后总利润不低于25%,那么每套悠悠球的售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
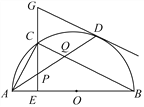
【题目】如图,在⊙O中,AB是直径,点D是⊙O上一点,点C是![]() 的中点,CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE,CB于点P,Q,连接AC,关于下列结论:①∠BAD=∠ABC;②GP=GD;③点P是△ACQ的外心,其中结论正确的是________(只需填写序号).
的中点,CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE,CB于点P,Q,连接AC,关于下列结论:①∠BAD=∠ABC;②GP=GD;③点P是△ACQ的外心,其中结论正确的是________(只需填写序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
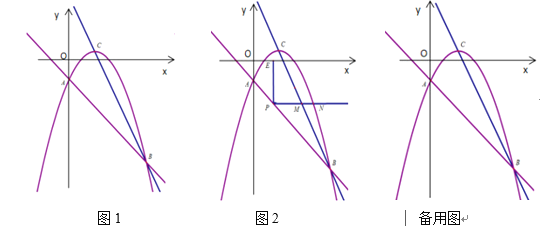
【题目】如图,直线![]() 与抛物线分别交于点A、点B,且点A在y轴上,抛物线的顶点C的坐标为
与抛物线分别交于点A、点B,且点A在y轴上,抛物线的顶点C的坐标为![]() .
.
(1)求抛物线的解析式;
(2)点P是线段AB上一动点,射线![]() 轴并与直线BC和抛物线分别交于点M、N,过点P作
轴并与直线BC和抛物线分别交于点M、N,过点P作![]() 轴于点E,当PE与PM的乘积最大时,在y轴上找一点Q,使
轴于点E,当PE与PM的乘积最大时,在y轴上找一点Q,使![]() 的值最大,求
的值最大,求![]() 的最大值和此时Q的坐标;
的最大值和此时Q的坐标;
(3)在抛物线上找一点D,使△ABD为直角三角形,求D点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com