
分析 首先用m表示出二次函数图象的对称轴,然后结合图象的单调性即可对①作出判断;
用m表示出图象与x轴的两交点的距离,再解出m的值即可对②作出判断;
先把二次函数y=x2-2mx-3化为顶点坐标式,根据函数最小值为4即可求出m的值,进而对③作出判断;
先求出对称轴为x=1008.5,然后可知x=2017时的函数值与x=0值相等,据此对④作出判断.
解答 解:①∵当x≤1时y随x的增大而减小,
∴函数的对称轴x=-$\frac{-2m}{2}$≥1在直线x=1的右侧(包括与直线x=1重合),
∴m≥1,故本选项错误;
②令y=x2-2mx-3=0,x1+x2=2m,x1x2=-3,
|x1-x2|2=(x1+x2)2-4x1x2=4m2+12=16,
解得m=±1,故本选项正确;
③二次函数y=x2-2mx-3=(x-m)2-m2-3,
当图象向左平移3个单位后的函数的最小值是-4,
则-m2-3=-4,
解得m=±1,故本选项错误;
④当x=1时的函数值与x=2017时的函数值相等,
则二次函数图象对称轴为x=1008.5,
则x=2017时的函数值与x=0值相等,
则当x=2017时的函数值为-3,故本选项正确;
故答案为②④.
点评 本题主要考查了二次函数的性质的知识,解答本题的关键是要掌握二次函数图象的对称轴,开口方向、函数的单调性等知识,此题难度不大.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
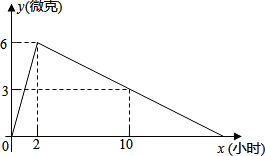 某医药研究所开发了一种新药,在试验药效时发现,如果成人按规定剂量服用,那么服药后2小时时血液中含药量最高,达每毫升6微克,接着逐步衰减,10小时血液中含药量为每毫升3微克,每毫升血液中含药量y微克随时间x小时主变化如图所示,当成人按规定剂是服药后,
某医药研究所开发了一种新药,在试验药效时发现,如果成人按规定剂量服用,那么服药后2小时时血液中含药量最高,达每毫升6微克,接着逐步衰减,10小时血液中含药量为每毫升3微克,每毫升血液中含药量y微克随时间x小时主变化如图所示,当成人按规定剂是服药后,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①②③ | B. | ②③④ | C. | ①③④ | D. | ①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
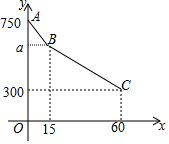 周末,小军在医院里照顾奶奶输液,小军问:“按照这样的输液速度,多少时间能结束输液?”护上答:“75分钟.”15分钟后,小军减慢了输液的速度,60分钟后,小军发现还剩有300毫升药液,剩下待输药液y(毫升)与输液时间x(分钟)的函数关系如图所示.
周末,小军在医院里照顾奶奶输液,小军问:“按照这样的输液速度,多少时间能结束输液?”护上答:“75分钟.”15分钟后,小军减慢了输液的速度,60分钟后,小军发现还剩有300毫升药液,剩下待输药液y(毫升)与输液时间x(分钟)的函数关系如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com