

分析 (1)作OH⊥PE,由PO是∠APE的角平分线,得到∠APO=∠EPO,判断出△PAO≌△PHO,得到OH=OA,用“圆心到直线的距离等于半径”来得出直线PE是⊙O的切线;
(2)先利用切线的性质和△PBC的周长为4求出PA=2,再用三角函数求出OA,AG,然后用三角形相似,得到EH=2EG,AE=2EH,用勾股定理求出EG,即可.
解答 证明:(1)如图1,
作OH⊥PE,
∴∠OHP=90°,
∵∠PAE=90,
∴∠OHP=∠OAP,
∵PO是∠APE的角平分线,
∴∠APO=∠EPO,
在△PAO和△PHO中
$\left\{\begin{array}{l}{∠OHP=∠OAP}\\{∠OPH=∠OPA}\\{OP=OP}\end{array}\right.$,
∴△PAO≌△PHO,
∴OH=OA,
∵OA是⊙O的半径,
∴OH是⊙O的半径,
∵OH⊥PE,
∴直线PE是⊙O的切线.
(2)如图2,连接GH,OH;
∵BC,PA,PB是⊙O的切线,
∴DB=BA,DC=CH,
∵△PBC的周长为4,
∴PB+PC+BC=4,
∴PB+PC+DB+DC=4,
∴PB+AB+PC+CH=4,
∴PA+PH=4,
∵PA,PH是⊙O的切线,
∴PA=PH,
∴PA=2,
由(1)得,△PAO≌△PHO,
∴∠OFA=90°,
∴∠EAH+∠AOP=90°,
∵∠OAP=90°,
∴∠AOP+∠APO=90°,
∴∠APO=∠EAH,
∵tan∠EAH=$\frac{1}{2}$,
∴tan∠APO=$\frac{OA}{PA}$=$\frac{1}{2}$,
∴OA=$\frac{1}{2}$PA=1,
∴AG=2,
∵∠AHG=90°,
∵tan∠EAH=$\frac{GH}{AH}$=$\frac{1}{2}$,
∵△EGH∽△EHA,
∴$\frac{EG}{EH}$=$\frac{EH}{AE}$=$\frac{GH}{AH}$=$\frac{1}{2}$,
∴EH=2EG,AE=2EH,
∴AE=4EG,
∵AE=EG+AG,
∴EG+AG=4EG,
∴EG=$\frac{1}{3}$AG=$\frac{2}{3}$,
∴EH=2EG=2×$\frac{2}{3}$=$\frac{4}{3}$.
点评 此题是切线的性质和判定题,主要考查了切线的判定和性质,相似三角形的性质和判定,勾股定理,三角函数,解本题的关键是用三角函数求出OA.


科目:初中数学 来源: 题型:解答题
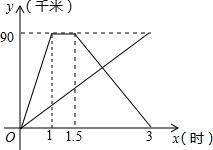 甲、乙两个人同时从相距90千米的A地前往B点,甲乘汽车,乙骑摩托车,甲到达B地停留半个小时后返回A地,如图是他们 离A地的距离y(千米)与时间x(时)之间的函数关系图象.
甲、乙两个人同时从相距90千米的A地前往B点,甲乘汽车,乙骑摩托车,甲到达B地停留半个小时后返回A地,如图是他们 离A地的距离y(千米)与时间x(时)之间的函数关系图象.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
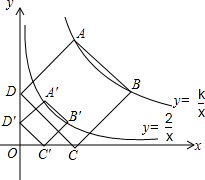 如图,正方形ABCD的顶点A,B在函数y=$\frac{k}{x}$(x>0)的图象上,点C,D分别在x轴,y轴的正半轴上,当k的值改变时,正方形ABCD的大小也随之改变.
如图,正方形ABCD的顶点A,B在函数y=$\frac{k}{x}$(x>0)的图象上,点C,D分别在x轴,y轴的正半轴上,当k的值改变时,正方形ABCD的大小也随之改变.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
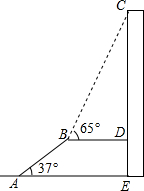 如图,AB是长为10m,倾斜角为37°的自动扶梯,平台BD与大楼CE垂直,且与扶梯AB的长度相等,在B处测得大楼顶部C的仰角为65°,求大楼CE的高度(结果保留整数).
如图,AB是长为10m,倾斜角为37°的自动扶梯,平台BD与大楼CE垂直,且与扶梯AB的长度相等,在B处测得大楼顶部C的仰角为65°,求大楼CE的高度(结果保留整数).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
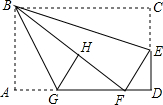 如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:
如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
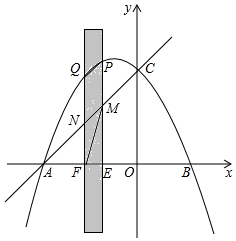 如图,抛物线与x轴交于点A(-5,0)和点B(3,0).与y轴交于点C(0,5).有一宽度为1,长度足够的矩形(阴影部分)沿x轴方向平移,与y轴平行的一组对边交抛物线于点P和Q,交直线AC于点M和N.交x轴于点E和F.
如图,抛物线与x轴交于点A(-5,0)和点B(3,0).与y轴交于点C(0,5).有一宽度为1,长度足够的矩形(阴影部分)沿x轴方向平移,与y轴平行的一组对边交抛物线于点P和Q,交直线AC于点M和N.交x轴于点E和F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=2$\sqrt{3}$,则阴影部分的面积为( )
如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=2$\sqrt{3}$,则阴影部分的面积为( )| A. | 2π | B. | π | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | -$\frac{1}{4}$ | C. | 4 | D. | -1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com