
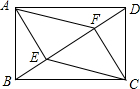
 如图,在矩形ABCD中,BD为对角线,点E,F是线段BD上的点,且BE=DF,连接AE,EC,CF,FA.
如图,在矩形ABCD中,BD为对角线,点E,F是线段BD上的点,且BE=DF,连接AE,EC,CF,FA.分析 (1)连接AC,交BD于点O,由矩形的性质得出AO=CO,BO=DO,证出EO=FO即可;
(2)根据菱形的性质和等腰直角三角形的性质即可求得AD..
解答 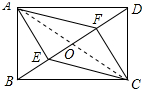 (1)证明:连接AC,交BD于点O,如图所示:
(1)证明:连接AC,交BD于点O,如图所示:
∵四边形ABCD是矩形,
∴AO=CO,BO=DO.
又∵BE=DF,
∴EO=FO.
∴四边形AECF是平行四边形;
(2)解:∵?AECF为菱形,
∴AC⊥EF,
∵AO=BO,AB=4,
∴BO=4×$\frac{\sqrt{2}}{2}$=2$\sqrt{2}$,
∴BD=4$\sqrt{2}$,
∴AD=4.
点评 本题考查了平行四边形的判定方法、矩形的性质、菱形的判定和性质;熟练掌握矩形的性质和平行四边形的判定方法、菱形的判定和性质是解决问题的关键.


 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:初中数学 来源: 题型:解答题
 如图,在单位正方形网格中,建立了平面直角坐标系xOy,试解答下列问题:
如图,在单位正方形网格中,建立了平面直角坐标系xOy,试解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
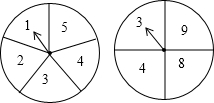 如图,图中的两个转盘分别被均匀地分成5个和4个扇形,每个扇形上都标有数字,同时自由转动两个转盘,转盘停止后,指针都落在偶数上的概率是( )
如图,图中的两个转盘分别被均匀地分成5个和4个扇形,每个扇形上都标有数字,同时自由转动两个转盘,转盘停止后,指针都落在偶数上的概率是( )| A. | $\frac{3}{20}$ | B. | $\frac{3}{10}$ | C. | $\frac{1}{5}$ | D. | $\frac{2}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 177×104 | B. | 17.7×105 | C. | 1.77×106 | D. | 0.177×107 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
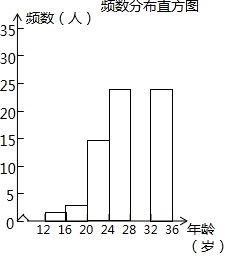 从共享单车,共享汽车等共享出行到共享雨伞等共享物品,各式各样的共享经济模式在各个领域迅速的普及,根据国家信息中心发布的中国分享经济发展报告2017显示,参与共享经济活动超6 亿人,比上一年增加约1亿人.
从共享单车,共享汽车等共享出行到共享雨伞等共享物品,各式各样的共享经济模式在各个领域迅速的普及,根据国家信息中心发布的中国分享经济发展报告2017显示,参与共享经济活动超6 亿人,比上一年增加约1亿人.| 年龄段(岁) | 频数 | 频率 |
| 12≤x<16 | 2 | 0.02 |
| 16≤x<20 | 3 | 0.03 |
| 20≤x<24 | 15 | a |
| 24≤x<28 | 25 | 0.25 |
| 28≤x<32 | b | 0.30 |
| 32≤x<36 | 25 | 0.25 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com