
 如图,AB是⊙O的直径,M是⊙O上一点,MN⊥AB,垂足为N.P,Q分别为弧AM,弧BM上一点(不与端点重合),如果∠MNP=∠MNQ.有以下结论:①∠1=∠2,②∠MPN+∠MQN=180°,③∠MQN=∠PMN,④PM=QM,⑤MN2=PN•QN.其中正确的是①③⑤.
如图,AB是⊙O的直径,M是⊙O上一点,MN⊥AB,垂足为N.P,Q分别为弧AM,弧BM上一点(不与端点重合),如果∠MNP=∠MNQ.有以下结论:①∠1=∠2,②∠MPN+∠MQN=180°,③∠MQN=∠PMN,④PM=QM,⑤MN2=PN•QN.其中正确的是①③⑤. 分析 利用等角的余角相等得到①对;利用三角形内角和定理得②错;利用垂径定理,同弧所对的圆周角相等得③对;利用三角形相似得⑤对,④错.
解答 解:延长QN交圆O于C,延长MN交圆O于D,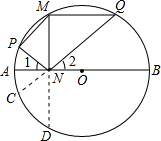 如图,
如图,
∵MN⊥AB,∠MNP=∠MNQ,
则∠1=∠2,故①正确;
∵AB是⊙O的直径,MN⊥AB,$\widehat{AM}$=$\widehat{DA}$,
∵∠1=∠2,∠ANC=∠2,
∴∠1=∠ANC,
∴P,C关于AB对称,
则$\widehat{PA}$=$\widehat{AC}$,$\widehat{PD}$=$\widehat{MC}$,
∴∠MQN=∠PMN,故③正确;
∵∠MPN+∠PMN<180°,∠MQN=∠PMN,
∴∠MPN+∠MQN<180°,
故②错误;
∵∠MNP=∠MNQ,∠Q=∠PMN,
∴△PMN∽△MQN,
∴MN2=PN•QN,PM不一定等于MQ;
故⑤正确,④错误.
故答案为:①③⑤.
点评 此题为圆的综合题,考查了垂径定理、圆周角定理、相似三角形的判定与性质以及等腰三角形的性质等知识,此题综合性较强,难度适中,解题的关键是注意数形结合思想的应用,注意辅助线的作法.


科目:初中数学 来源: 题型:选择题
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,顶点为A(-4,4)的二次函数图象经过原点(0,0),点P在该图象上,OP交其对称轴l于点M,点M、N关于点A对称,连接PN,ON.
如图,顶点为A(-4,4)的二次函数图象经过原点(0,0),点P在该图象上,OP交其对称轴l于点M,点M、N关于点A对称,连接PN,ON.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标中,过点A(4,0)的抛物线y=-x2+bx与直线y=-x+b交于另一点B.过抛物线y=-x2+bx的顶点E作EF⊥x轴于F点,点M(t,d)为抛物线y=-x2+bx在x轴上方的动点.
如图,在平面直角坐标中,过点A(4,0)的抛物线y=-x2+bx与直线y=-x+b交于另一点B.过抛物线y=-x2+bx的顶点E作EF⊥x轴于F点,点M(t,d)为抛物线y=-x2+bx在x轴上方的动点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 重庆是一座美丽的山城,某中学依山而建,校门A处,有一斜坡AB,长度为13米,在斜坡B处看教学楼CF的楼顶C的仰角∠CBF=53°,离B点4米远的E处有一花台,在E处仰望C的仰角∠CEF=63.4°,CF的延长线交校门处的水平面于D点,FD=5米
重庆是一座美丽的山城,某中学依山而建,校门A处,有一斜坡AB,长度为13米,在斜坡B处看教学楼CF的楼顶C的仰角∠CBF=53°,离B点4米远的E处有一花台,在E处仰望C的仰角∠CEF=63.4°,CF的延长线交校门处的水平面于D点,FD=5米查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com