
【题目】如图,点![]() 是等边
是等边![]() 内一点,
内一点,![]() .将
.将![]() 绕点
绕点![]() 按顺时针方向旋转
按顺时针方向旋转![]() 得
得![]() ,连接
,连接![]() .
.

(1)求证:![]() 是等边三角形;
是等边三角形;
(2)当![]() 时,试判断
时,试判断![]() 的形状,并说明理由;
的形状,并说明理由;
(3)探究:当![]() 为多少度时,
为多少度时,![]() 是等腰三角形?
是等腰三角形?
【答案】(1)见解析(2)直角三角形;(3)![]() 为110°、125°、140°
为110°、125°、140°
【解析】
试题(1)由△BOC≌△ADC,得出CO=CD,再由∠OCD=60°,得出结论;
(2)由勾股定理的逆定理判断△AOD为直角三角形;
(3)因为△AOD是等腰三角形,可得①∠AOD=∠ADO、②∠ODA=∠OAD、③∠AOD=∠DAO;若∠AOB=110°,∠COD=60°,∠BOC=190°-∠AOD,∠BOC=∠ADC=∠ADO+∠CDO由①∠AOD=∠ADO可得α=125°,由②∠ODA=∠OAD可得α=110°,由③∠AOD=∠DAO可得α=140°.
试题解析:(1)∵将△BOC绕点C按顺时针方向旋转60°得△ADC,
∴△BOC≌△ADC,∠OCD=60°,
∴CO=CD.
∴△COD是等边三角形.
(2)△AOD为直角三角形,
∵△ADC≌△BOC,
∴DA=OB=5,
∵△COD是等边三角形,
∴OD=OC=4,又OA=3,
∴DA2=OA2+OD2,
∴△AOD为直角三角形.
(3)因为△AOD是等腰三角形,
所以分三种情况:①∠AOD=∠ADO②∠ODA=∠OAD③∠AOD=∠DAO
∵∠AOB=110°,∠COD=60°,
∴∠BOC=190°-∠AOD,
而∠BOC=∠ADC=∠ADO+∠CDO
由①∠AOD=∠ADO可得∠BOC=∠AOD+60°,求得α=125°;
由②∠ODA=∠OAD可得∠BOC=150°-![]() ∠AOD,求得α=110°;
∠AOD,求得α=110°;
由③∠AOD=∠DAO可得∠BOC=240°-2∠AOD,求得α=140°;
综上可知α=125°、α=110°或α=140°.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
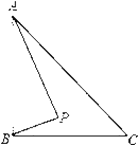
【题目】如图,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP长的最小值为( )
A. 2 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在北京市开展的“首都少年先锋岗”活动中,某数学小组到人民英雄纪念碑站岗执勤,并在活动后实地测量了纪念碑的高度. 方法如下:如图,首先在测量点A处用高为1.5m的测角仪AC测得人民英雄纪念碑MN顶部M的仰角为35°,然后在测量点B处用同样的测角仪BD测得人民英雄纪念碑MN顶部M的仰角为45°,最后测量出A,B两点间的距离为15m,并且N,B,A三点在一条直线上,连接CD并延长交MN于点E. 请你利用他们的测量结果,计算人民英雄纪念碑MN的高度.
(参考数据:sin35°≈0.6,cos35°≈0.8,tan35°≈0.7)


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是( )

A. 55° B. 60° C. 65° D. 70°
查看答案和解析>>
科目:初中数学 来源: 题型:
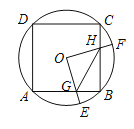
【题目】如图,边长为4的正方形ABCD内接于⊙O,点E是![]() 上的一动点(不与点A、B重合),点F是
上的一动点(不与点A、B重合),点F是![]() 上的一点,连接OE,OF,分别与交AB,BC于点G,H,且∠EOF=90°,连接GH,有下列结论:
上的一点,连接OE,OF,分别与交AB,BC于点G,H,且∠EOF=90°,连接GH,有下列结论:
①![]() ;②△OGH是等腰直角三角形;③四边形OGBH的面积随着点E位置的变化而变化;④△GBH周长的最小值为
;②△OGH是等腰直角三角形;③四边形OGBH的面积随着点E位置的变化而变化;④△GBH周长的最小值为![]() .其中正确的是____________.(把你认为正确结论的序号都填上)
.其中正确的是____________.(把你认为正确结论的序号都填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
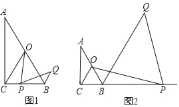
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=30°,点O为AB中点,点P为直线BC上的动点(不与点B、点C重合),连接OC、OP,将线段OP绕点P顺时针旋转60°,得到线段PQ,连接BQ.
(1)如图1,当点P在线段BC上时,试猜想写出线段CP与BQ的数量关系,并证明你的猜想;
(2)如图2,当点P在CB延长线上时,(1)中结论是否成立?(直接写“成立”或“不成立”即可,不需证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
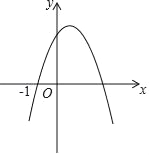
【题目】如图,函数y=ax2+bx+c的图象过点(﹣1,0)和(m,0),请思考下列判断:①abc<0;②4a+c<2b;③![]() =1﹣
=1﹣![]() ;④am2+(2a+b)m+a+b+c<0;⑤|am+a|=
;④am2+(2a+b)m+a+b+c<0;⑤|am+a|=![]() 正确的是( )
正确的是( )
A. ①③⑤ B. ①②③④⑤ C. ①③④ D. ①②③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=kx+b的图象与反比例函数y2=![]() 的图象交于点A(﹣3,2),B(n,﹣6)两点.
的图象交于点A(﹣3,2),B(n,﹣6)两点.
(1)求一次函数与反比例函数的解析式;
(2)求△AOB的面积;
(3)请直接写出y1<y2时x的范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com