
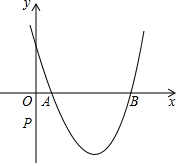
 已知二次函数图象的顶点坐标为C(3,-2),且在x轴上截得的线段AB长为4,在y轴上有一点P,使△APC的周长最小,求P点的坐标.
已知二次函数图象的顶点坐标为C(3,-2),且在x轴上截得的线段AB长为4,在y轴上有一点P,使△APC的周长最小,求P点的坐标. 分析 由抛物线的顶点坐标可得抛物线的对称轴为直线x=3,利用抛物线的对称性可得A点和B点坐标分别为(1,0),(5,0),作点A关于y轴的对称点A′,连接A′C交y轴于点P,则点P即为所求,利用待定系数法求出直线A′C的解析式,得出P点坐标即可.
解答  解:∵抛物线的顶点坐标为C(3,-2),
解:∵抛物线的顶点坐标为C(3,-2),
∴抛物线的对称轴为直线x=3,
∵二次函数的图象在x轴上截得的线段AB长为4,
∴A点和B点坐标分别为(1,0),(5,0).
作点A关于y轴的对称点A′,连接A′C交y轴于点P,则点P即为所求,则A′(-1,0),
设直线A′C的解析式为y=kx+b(k≠0),
∵A′(-1,0),C(3,-2),
∴$\left\{\begin{array}{l}{-k+b=0}\\{3k+b=-2}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=-\frac{1}{2}}\end{array}\right.$,
∴直线A′C的解析式为y=-$\frac{1}{2}$x-$\frac{1}{2}$,
∴当x=0时,y=-$\frac{1}{2}$,
∴P(0,-$\frac{1}{2}$).
点评 本题考查的是抛物线与x轴的交点,先根据题意得出A、B两点的坐标是解答此题的关键.


科目:初中数学 来源: 题型:选择题
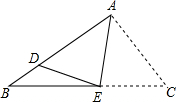 如图,△ABC中,∠ABC=30°,∠ACB=50°,折叠△ACB使点C与AB边上的点D重合,折痕为AE,连DE,则∠AED为( )
如图,△ABC中,∠ABC=30°,∠ACB=50°,折叠△ACB使点C与AB边上的点D重合,折痕为AE,连DE,则∠AED为( )| A. | 70° | B. | 75° | C. | 80° | D. | 85° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 调查“神州十一号飞船”各部分零件情况 | |
| B. | 调查旅客随身携带的违禁物品 | |
| C. | 调查全国高中学生对“数学核心素养”的了解 | |
| D. | 调查某校九年级(1)班学生中考体育成绩 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
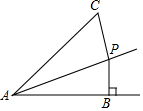 如图,点P是∠BAC的平分线上一点,PB⊥AB于B,且PB=5cm,AC=12,则△APC的面积是( )
如图,点P是∠BAC的平分线上一点,PB⊥AB于B,且PB=5cm,AC=12,则△APC的面积是( )| A. | 30cm2 | B. | 40cm2 | C. | 50cm2 | D. | 60cm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
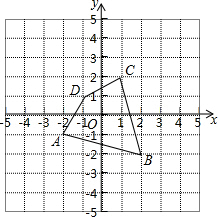 如图,在平面直角坐标系中,O为坐标原点,每个小方格的边长为1个单位长度.四边形ABCD顶点都在格点上,点A的坐标为(-2,-1)
如图,在平面直角坐标系中,O为坐标原点,每个小方格的边长为1个单位长度.四边形ABCD顶点都在格点上,点A的坐标为(-2,-1)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
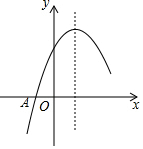 如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-1,0),对称轴为直线x=1,给出以下结论:
如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-1,0),对称轴为直线x=1,给出以下结论:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
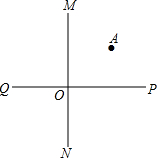 如图所示,直线MN⊥PQ,垂足是点O,点A是∠POM内部的任意一点.
如图所示,直线MN⊥PQ,垂足是点O,点A是∠POM内部的任意一点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
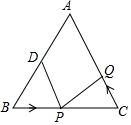 △ABC中,AB=AC=12厘米,∠B=∠C,BC=8厘米,点D为AB的中点.如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为v厘米/秒,则当△BPD与△CQP全等时,v的值为( )
△ABC中,AB=AC=12厘米,∠B=∠C,BC=8厘米,点D为AB的中点.如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为v厘米/秒,则当△BPD与△CQP全等时,v的值为( )| A. | 2 | B. | 5 | C. | 1或5 | D. | 2或3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com