
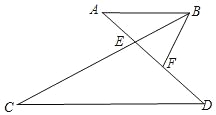
【题目】如图,已知AB∥CD,AD、BC相交于点E,点F在ED上,且∠CBF=∠D.
(1)求证:FB2=FEFA;
(2)若BF=3,EF=2,求△ABE与△BEF的面积之比.
【答案】(1)证明见解析;(2)5:4.
【解析】
试题分析:(1)要证明FB2=FEFA,只要证明△FBE∽△FAB即可,根据题目中的条件可以找到两个三角形相似的条件,本题得以解决;
(2)根据(1)中的结论可以得到AE的长,然后根据△ABE与△BEF如果底边分别为AE和EF,则底边上的高相等,面积之比就是AE和EF的比值.
试题解析:(1)∵AB∥CD,
∴∠A=∠D.
又∵∠CBF=∠D,
∴∠A=∠CBF,
∵∠BFE=∠AFB,
∴△FBE∽△FAB,
∴![]()
∴FB2=FEFA;
(2)∵FB2=FEFA,BF=3,EF=2
∴32=2×(2+AE)
∴![]()
∴![]() ,
,
∴△ABE与△BEF的面积之比为5:4.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠A=∠C=90°,BE,DF分别是∠ABC,∠ADC的平分线.

(1)∠1与∠2有什么关系,为什么?
(2)BE与DF有什么关系?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面去括号正确的是( )
A. x2-(3x-2)=x2-3x-2
B. 7a+(5b-1)=7a+5b+1
C. 2m2-(3m+5)=2m2-3m-5
D. -(a-b)+(ab-1)=a-b+ab-1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两艘客轮同时离开港口,航行的速度都是40m/min,甲客轮用15min到达点A,乙客轮用20min到达点B,若A,B两点的直线距离为1000m,甲客轮沿着北偏东30°的方向航行,则乙客轮的航行方向可能是( )
A. 北偏西30° B. 南偏西30° C. 南偏东60° D. 南偏西60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商贩同时卖出2件大衣,每件以240元成交,按成本价计算,其中一件盈利20%,另一件亏本20%,则这笔生意对于商贩来说是( )
A. 不赔不赚 B. 赔20元 C. 赚20元 D. 赔10元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各组线段,能组成三角形的是( )
A. 2cm,3cm,5cm B. 5cm,6cm,10cm
C. 1cm,1cm,3cm D. 3cm,4cm,8cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com