
【题目】在平面直角坐标系![]() 中,点
中,点![]() 在抛物线
在抛物线![]() 上.
上.
(1)如图1,若抛物线经过点![]() .
.
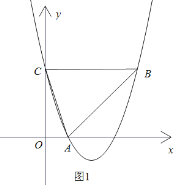
①求抛物线的解析式;
②设抛物线与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,若点
,若点![]() 在抛物线上,且
在抛物线上,且![]() 与
与![]() 的面积相等,求点
的面积相等,求点![]() 的坐标;
的坐标;
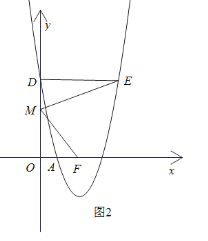
(2)如图2,若抛物线与![]() 轴交于点D过点
轴交于点D过点![]() 作
作![]() 轴的平行线交抛物线于另一点
轴的平行线交抛物线于另一点![]() .点
.点![]() 为抛物线的对称轴与
为抛物线的对称轴与![]() 轴的交点,
轴的交点,![]() 为线段
为线段![]() 上一动点.若以M,D,E为顶点的三角形与
上一动点.若以M,D,E为顶点的三角形与![]() 相似.并且符合条件的点
相似.并且符合条件的点![]() 恰有
恰有![]() 个,请直接写出抛物线的解析式及相应的点
个,请直接写出抛物线的解析式及相应的点![]() 的坐标.
的坐标.
【答案】(1)①![]() ;②
;②![]() ;(2)当抛物线的解析式为
;(2)当抛物线的解析式为![]() 时,点
时,点![]() 的坐标为
的坐标为![]() 或
或![]() ;当抛物线
;当抛物线![]() 的解析式为时,点
的解析式为时,点![]() 的坐标为
的坐标为![]() 或
或![]()
【解析】
(1)①利用待定系数法直接求抛物线的解析式;
②先求解![]() 的面积为
的面积为![]() 分情况讨论:当
分情况讨论:当![]() 在
在![]() 的下方时,过点
的下方时,过点![]() 作
作![]() 轴交
轴交![]() 于
于![]() ,设点
,设点![]() 利用
利用![]() 的面积为
的面积为![]() ,建立方程求解即可,当
,建立方程求解即可,当![]() 在
在![]() 的上方时,过点
的上方时,过点![]() 作
作![]() 的平行线,与抛物线的另一交点即为点
的平行线,与抛物线的另一交点即为点![]() ,利用函数的交点可得答案;
,利用函数的交点可得答案;
(2)先求解抛物线的解析式为:![]() ,得到
,得到![]() .
.
设![]() ,利用相似三角形的性质建立方程,由方程解的情况讨论得出结论.
,利用相似三角形的性质建立方程,由方程解的情况讨论得出结论.
解:![]() ①
①![]() 抛物线过点
抛物线过点![]() 和点
和点![]()
![]()
解得![]()
![]() 抛物线的解析式为
抛物线的解析式为![]()
②在![]() 中,令
中,令![]() 得
得![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]()
![]()
点![]() 到
到![]() 的距离为
的距离为![]()
![]()
设直线![]() 的解析式为
的解析式为![]()
则![]()
解得![]()
![]() 直线
直线![]() 的解析式为
的解析式为![]()
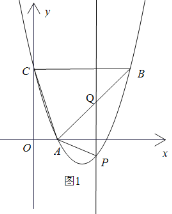
(I)如图,若点![]() 在直线
在直线![]() 下方的抛物线上,过点
下方的抛物线上,过点![]() 作
作![]() 轴交
轴交![]() 于
于![]()
设点![]()
则点![]()
![]()
![]() 无解
无解
此时点![]() 不存在
不存在
(II)若点![]() 在直线
在直线![]() 上方的抛物线上,过点
上方的抛物线上,过点![]() 作
作![]() 的平行线,与抛物线的另一交点即为点
的平行线,与抛物线的另一交点即为点![]() ,则
,则![]()
则可设直线![]() 的解析式为
的解析式为![]()
将![]() 代入,得
代入,得![]()
![]() 直线
直线![]() 的解析式为
的解析式为![]()
令![]()
解得![]() 或
或![]() (舍去
(舍去![]() )
)
![]()

![]() 当抛物线的解析式为
当抛物线的解析式为![]() 时,点
时,点![]() 的坐标为
的坐标为![]() 或
或![]()
当抛物线的解析式为![]() 时,点
时,点![]() 的坐标为
的坐标为![]() 或
或![]()
理由如下:由点![]() 在拋物线
在拋物线![]() 上,得
上,得![]()
![]() 抛物线的解析式为
抛物线的解析式为![]()
![]()
设![]()
当![]() 时,
时,![]()
即![]()
![]()
当![]() 时,
时,![]()
即![]()
![]()
![]() 当方程
当方程![]() 有两个相等实数根时,
有两个相等实数根时,
![]()
解得![]() (负值舍去)
(负值舍去)
此时,方程![]() 有两个相等实数根
有两个相等实数根![]()
方程![]() 有一个实数根
有一个实数根![]() ,符合题意
,符合题意
此时抛物线的解析式为![]()
点![]() 的坐标为
的坐标为![]() 或
或
![]() 当方程
当方程![]() 有两个不相等的实数根时,
有两个不相等的实数根时,
把![]() 代入
代入![]() ,解得
,解得![]() 负值舍去)
负值舍去)
此时,方程![]() 有两个不相等的实数根
有两个不相等的实数根![]()
方程![]() 有一个实数根
有一个实数根![]() ,符合题意;
,符合题意;
此时抛物线的解析式为![]()
点![]() 的坐标为
的坐标为![]() 或
或![]()
综上所述,当抛物线的解析式为![]()
点![]() 的坐标为
的坐标为![]() 或
或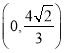 ;
;
当抛物线的解析式为![]() 时,
时,
点![]() 的坐标为
的坐标为![]() 或
或![]()


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:
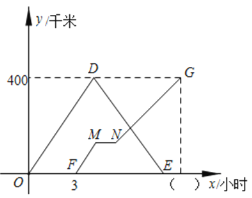
【题目】甲车从A地出发匀速驶向B地,到达B地后,立即按原路原速返回A地;乙车从B地出发沿相同路线匀速驶向A地,出发t(t>0)小时后,乙车因故在途中停车1小时,然后继续按原速驶向A地,乙车在行驶过程中的速度是80千米/时,甲车比乙车早1小时到达A地,两车距各自出发地的路程y千米与甲车行驶时间x小时之间的函数关系如图所示,请结合图象信息,解答下列问题:
(1)写出甲车行驶的速度,并直接在图中的( )内填上正确的数;
(2)求甲车从B地返回A地的过程中,y与x的函数解析式(不需要写出自变量x的取值范围);
(3)若从乙车出发至甲车到达A地,两车恰好有两次相距80千米,直接写出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
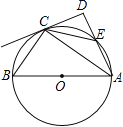
【题目】如图,AB是⊙O的直径,C是⊙O上的一点,过点A作AD⊥CD于点D,交⊙O于点E,且![]() =
=![]() .
.
(1)求证:CD是⊙O的切线;
(2)若tan∠CAB=![]() ,BC=3,求DE的长.
,BC=3,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
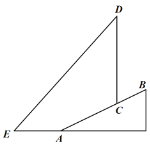
【题目】为践行“绿水青山就是金山银山”的重要思想,某森林保护区开展了寻找古树活动.如图,在一个坡度(或坡比)i=1:2.4的山坡AB上发现有一棵古树CD.测得古树底端C到山脚点A的距离AC=26米,在距山脚点A水平距离6米的点E处,测得古树顶端D的仰角∠AED=48°(古树CD与山坡AB的剖面、点E在同一平面上,古树CD与直线AE垂直),则古树CD的高度约为多少米?(参考数据:sin48°≈0.73,cos48°≈0.67,tan48°≈1.11)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 经过
经过![]() 的三个顶点,与
的三个顶点,与![]() 轴相交于
轴相交于![]() ,点
,点![]() 坐标为
坐标为![]() ,点
,点![]() 是点
是点![]() 关于
关于![]() 轴的对称点,点
轴的对称点,点![]() 在
在![]() 轴的正半轴上.
轴的正半轴上.
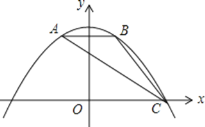
(1)求该抛物线的函数解析式;
(2)点![]() 为线段
为线段![]() 上一动点,过点
上一动点,过点![]() 作
作![]() 轴,
轴,![]() 轴, 垂足分别为点
轴, 垂足分别为点![]() ,
,![]() ,当四边形
,当四边形![]() 为正方形时,求出点
为正方形时,求出点![]() 的坐标;
的坐标;
(3)将(2) 中的正方形![]() 沿
沿![]() 向右平移,记平移中的正方形
向右平移,记平移中的正方形![]() 为正方形
为正方形![]() ,当点
,当点![]() 和点
和点![]() 重合时停止运动, 设平移的距离为
重合时停止运动, 设平移的距离为![]() ,正方形的边
,正方形的边![]() 与
与![]() 交于点
交于点![]() ,
,![]() 所在的直线与
所在的直线与![]() 交于点
交于点![]() , 连接
, 连接![]() ,是否存在这样的
,是否存在这样的![]() ,使
,使![]() 是等腰三角形?若存在,求
是等腰三角形?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:函数![]() 与
与![]() 的图象关于
的图象关于![]() 轴对称,点
轴对称,点![]() 是
是![]() 轴上一点,将函数
轴上一点,将函数![]() 的图象位于直线
的图象位于直线![]() 左侧的部分,以
左侧的部分,以![]() 轴为对称轴翻折,得到新的函数
轴为对称轴翻折,得到新的函数![]() 的图象,我们称函数
的图象,我们称函数![]() 是函数
是函数![]() 的对称折函数,函数
的对称折函数,函数![]() 的图象记作
的图象记作![]() ,函数
,函数![]() 的图象位于直线
的图象位于直线![]() 上以及右侧的部分记作
上以及右侧的部分记作![]() ,图象
,图象![]() 和
和![]() 合起来记作图象
合起来记作图象![]() .
.
例如:如图,函数![]() 的解析式为
的解析式为![]() ,当
,当![]() 时,它的对称折函数
时,它的对称折函数![]() 的解析式为
的解析式为![]() .
.
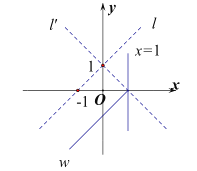
(1)函数![]() 的解析式为
的解析式为![]() ,当
,当![]() 时,它的对称折函数
时,它的对称折函数![]() 的解析式为_______;
的解析式为_______;
(2)函数![]() 的解析式为
的解析式为![]() ,当
,当![]() 且
且![]() 时,求图象
时,求图象![]() 上点的纵坐标的最大值和最小值;
上点的纵坐标的最大值和最小值;
(3)函数![]() 的解析式为
的解析式为![]() .若
.若![]() ,直线
,直线![]() 与图象
与图象![]() 有两个公共点,求
有两个公共点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:二次函数y=x2-2mx-m2+4m-2的对称轴为l,抛物线与y轴交于点C,顶点为D.

(1)判断抛物线与x轴的交点情况;
(2)如图1,当m=1时,点P为第一象限内抛物线上一点,且△PCD是以PD为腰的等腰三角形,求点P的坐标;
(3)如图2,直线![]() 和抛物线交于点A、B两点,与l交于点M,且MO=MB,点Q(x0,y0)在抛物线上,当m>1时,
和抛物线交于点A、B两点,与l交于点M,且MO=MB,点Q(x0,y0)在抛物线上,当m>1时,![]() 时,求h的最大值.
时,求h的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com