Question

如图，在△ABC中，AB＝AC，以AB为直径的⊙O分别交AC、BC于点M、N，在AC的延长线上取点P，使∠CBP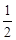＝∠A．

【小题1】（1）判断直线BP与⊙O的位置关系，并证明你的结论；
【小题2】（2）若⊙O的半径为1，tan∠CBP＝0.5，求BC和BP的长．

Answer 1

【小题1】⑴相切.
证明：连结AN，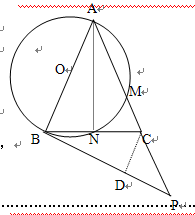

∵AB是直径，
∴∠ANB=90°.
∵AB=AC，
∴∠BAN=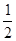∠A=∠CBP.
又∵∠BAN+∠ABN=180°-∠ANB= 90°，
∴∠CBP+∠ABN=90°，即AB⊥BP.
∵AB是⊙O的直径，
∴直线BP与⊙O相切.
【小题2】 ⑵∵在Rt△ABN中，AB=2，tan∠BAN= tan∠CBP=0.5，
可求得，BN=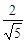，∴BC=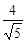.        …………………………………………4分
作CD⊥BP于D，则CD∥AB，.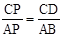
在Rt△BCD中，易求得CD=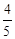，BD=.     …………………………………5分
代入上式，得=.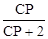
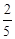∴CP=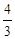.                          …………………………………………6分
∴DP=.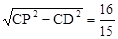
∴BP=BD+DP=+=. 

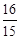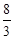解析