
| c-1 |
| a-2 |
| b+1 |
c2-2
|
| c-1 |
| a-2 |
| b+1 |
| a-2 |
| b+1 |
| c-1 |
| c-1 |
| a-2 |
| b+1 |
| c-1 |
| a-2 |
| b+1 |
| a-2 |
| b+1 |
| c-1 |
| a-2 |
| a-2 |
| b+1 |
| b+1 |
| c-1 |
| a-2 |
| b+1 |
| c-1 |
| a-2 |
| b+1 |
| c-1 |
| a-2 |
| b+1 |
| c-1 |
c2-2
|
22-2
|
5-2
|
(
|
| 3 |
| 2 |


科目:初中数学 来源: 题型:
| A、不超过9999 |
| B、在10000到99999之间 |
| C、在100000到999999之间 |
| D、在1000000到9999999之间 |
查看答案和解析>>
科目:初中数学 来源: 题型:
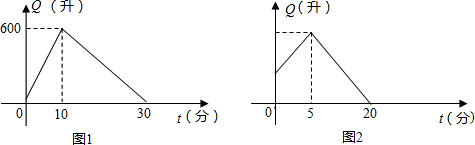
查看答案和解析>>
科目:初中数学 来源: 题型:
 九年级(1)班为即将到来的“五•一”国际劳动节排练节目时需要3个底面圆半径为10厘米,母线长为20厘米的圆锥形小红帽(不计接缝损失).
九年级(1)班为即将到来的“五•一”国际劳动节排练节目时需要3个底面圆半径为10厘米,母线长为20厘米的圆锥形小红帽(不计接缝损失).查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,有一棱长为3的正方体,将其每个面画上黑线分成9个边长相等的小正方形.现在沿画曲线的小正方形的四边向下打孔,使正方体被打出一个方孔.然后将这个被打方孔的正方体浸没在一盆绿水中,于是它被染绿了.接着沿所有的黑线将正方体切开.则仅有一面是绿色的小正方体有
如图,有一棱长为3的正方体,将其每个面画上黑线分成9个边长相等的小正方形.现在沿画曲线的小正方形的四边向下打孔,使正方体被打出一个方孔.然后将这个被打方孔的正方体浸没在一盆绿水中,于是它被染绿了.接着沿所有的黑线将正方体切开.则仅有一面是绿色的小正方体有查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com