
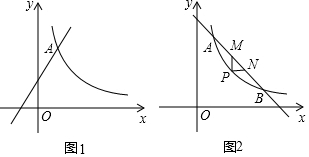
分析 (1)利用待定系数法即可得出结论;
(2)先表示出点C,D的坐标,再判断出点E是线段CD的中点,利用中点坐标公式即可求出t的值;
(3)先设出点P的坐标,进而表示出点M,N的坐标,即可得出PM,PN,再判断出△PMN是等腰直角三角形,
进而判断出PN越小,三角形PMN的面积越小,即可求出a的值,即可.
解答 解:(1)∵点A(a,6)在直线l:y=$\frac{3}{2}$x+3上,
∴6=$\frac{3}{2}$a+3,
∴a=2,
∴A(2,6),
∵点A在双曲线y=$\frac{k}{x}$上,
∴k=2×6=12,
∴反比例函数解析式为y=$\frac{12}{x}$;
(2)如图2,
由(1)知,双曲线的解析式为y=$\frac{12}{x}$,
∵D(t,$\frac{12}{t}$),
∵点C在直线l:y=$\frac{3}{2}$x+3上,
∴C(t,$\frac{3}{2}$t+3),
过点A作AE⊥CD于E,
∴E(t,6),
∵AC=AD,
∴点E是CD的中点,A(2,6),
∴$\frac{12}{t}$+$\frac{3}{2}$t+3=2×6,
∴t=2(舍)或t=4,
(3)如图2,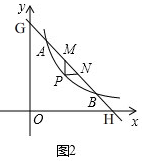 由(1)知,A(2,6),
由(1)知,A(2,6),
∵直线m:y=-x+c,过点A,
∴-2+c=6,
∴c=8,
∴直线m:y=-x+8,
∴∠OHG=∠OGH=45°,
由(1)知,双曲线:y=$\frac{12}{x}$,
∵点P在双曲线上,
∴设P(a,$\frac{12}{a}$),(2≤a≤6),
∵PM∥y轴,且M在直线m上,
∴∠PMN=45°,M(a,a+8),
∵PN∥x轴,且N在直线m上,
∴∠PNM=45°,N(8-$\frac{12}{a}$,$\frac{12}{a}$),
∵点M,N在线段AB上,
∴PN=8-$\frac{12}{a}$-a=8-(a+$\frac{12}{a}$),
易知,△PMN是等腰直角三角形,
∴S△PMN=$\frac{1}{2}$PN2=$\frac{1}{2}$[8-(a+$\frac{12}{a}$)]2,
由于a+$\frac{12}{a}$>0,只要a+$\frac{12}{a}$越小,S△PMN越大,
而a+$\frac{12}{a}$≥2•$\sqrt{a}$•$\sqrt{\frac{12}{a}}$=4$\sqrt{3}$(当且仅当$\sqrt{a}$=$\sqrt{\frac{12}{a}}$时,取等号,即:a=-2$\sqrt{3}$(舍)或a=2$\sqrt{3}$)
∴S△PMN最大=$\frac{1}{2}$(8-4$\sqrt{3}$)2=56-32$\sqrt{3}$.
点评 此题是反比例函数综合题,主要考查了待定系数法,线段的中点坐标的求法,等腰三角形的性质,等腰直角三角形的性质,解(2)的关键是判断出点E是线段CD的中点,解(3)的关键是确定出a的值,是一道中等难度的题目.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源: 题型:解答题
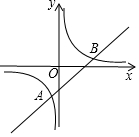 如图,在平面直角坐标系xOy中,直线y=kx-3与双曲线y=$\frac{4}{x}$的两个交点为A,B,其中A(-1,m).
如图,在平面直角坐标系xOy中,直线y=kx-3与双曲线y=$\frac{4}{x}$的两个交点为A,B,其中A(-1,m).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 班级 | 参加人数 | 中位数 | 方差 | 平均数 |
| (1)班 | 50 | 120 | 103 | 122 |
| (2)班 | 49 | 121 | 201 | 122 |
| A. | 两班平均成绩一样 | B. | (1)班的优秀人数多于(2)班 | ||
| C. | (2)班的两极分化比(1)班严重 | D. | (1)班的总体成绩稳定一些 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
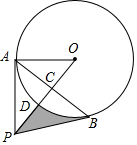 如图,点A在⊙O上,点P是⊙O外一点,PA切⊙O于点A,连接OP交⊙O于点D,作AB⊥OP于点C,交⊙O于点B,连接PB.
如图,点A在⊙O上,点P是⊙O外一点,PA切⊙O于点A,连接OP交⊙O于点D,作AB⊥OP于点C,交⊙O于点B,连接PB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某电视台的一档娱乐性节目中,在游戏PK环节,为了随机分选游戏双方的组员,主持人设计了以下游戏:用不透明的白布包住三根颜色长短相同的细绳AA1、BB1、CC1,只露出它们的头和尾(如图所示),由甲、乙两位嘉宾分别从白布两端各选一根细绳,并拉出,若两人选中同一根细绳,则两人同队,否则互为反方队员.
某电视台的一档娱乐性节目中,在游戏PK环节,为了随机分选游戏双方的组员,主持人设计了以下游戏:用不透明的白布包住三根颜色长短相同的细绳AA1、BB1、CC1,只露出它们的头和尾(如图所示),由甲、乙两位嘉宾分别从白布两端各选一根细绳,并拉出,若两人选中同一根细绳,则两人同队,否则互为反方队员.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com