
分析 把2,24,27,n分解为两个正整数的积的形式,找到相差最少的两个数,让较小的数除以较大的数,看结果是否与所给结果相同.
解答 解:∵2=1×2,
∴F(2)=$\frac{1}{2}$是正确的;
∵24=1×24=2×12=3×8=4×6,这几种分解中4和6的差的绝对值最小,
∴F(24)=$\frac{4}{6}$=$\frac{2}{3}$,故②是错误的;
∵27=1×27=3×9,其中3和9的绝对值较小,又3<9,
∴F(27)=$\frac{1}{3}$,故③是错误的;
∵n是一个完全平方数,
∴n能分解成两个相等的数,则F(n)=1,故④是正确的.
∴正确的有①④,
故答案为:①④.
点评 本题考查有理数的混合运算与信息获取能力,解决本题的关键是理解此题的定义:所有这种分解中两因数之差的绝对值最小,F(n)═$\frac{p}{q}$(p,q是正整数,且p≤q).


 优等生题库系列答案
优等生题库系列答案科目:初中数学 来源: 题型:填空题
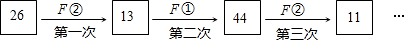
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
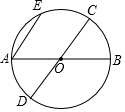 已知:如图,AB,CD是⊙O的直径,AE是⊙O的弦,若AE∥CD,求证:$\widehat{AD}$=$\widehat{BC}$=$\widehat{EC}$.
已知:如图,AB,CD是⊙O的直径,AE是⊙O的弦,若AE∥CD,求证:$\widehat{AD}$=$\widehat{BC}$=$\widehat{EC}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
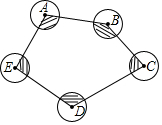 如图,⊙A、⊙B、⊙C、⊙D、⊙E的半径都是4cm,顺次连接五个圆心得到五边形ABCDE,则图中五个扇形(阴影部分)面积的和为24πcm2.
如图,⊙A、⊙B、⊙C、⊙D、⊙E的半径都是4cm,顺次连接五个圆心得到五边形ABCDE,则图中五个扇形(阴影部分)面积的和为24πcm2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com