
【题目】如图,四边形![]() 是
是![]() 的内接正方形,
的内接正方形,![]() ,
,![]() 、
、![]() 是
是![]() 的两 条切线,
的两 条切线,![]() 、
、![]() 为切点.
为切点.
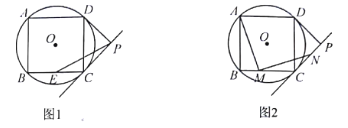
(1)如图1,求![]() 的半径;
的半径;
(2)如图1,若点![]() 是
是![]() 的中点,连结
的中点,连结![]() ,求
,求![]() 的长度;
的长度;
(3)如图2,若点![]() 是
是![]() 边上任意一点(不含
边上任意一点(不含![]() 、
、![]() ),以点
),以点![]() 为直角顶点,在
为直角顶点,在![]() 的上方作
的上方作![]() ,交直线
,交直线![]() 于点
于点![]() ,求证:
,求证:![]() .
.
【答案】(1)2![]() ;(2)
;(2)![]() ;(3)见解析.
;(3)见解析.
【解析】
(1)利用切线的性质以及正方形的判定与性质得出⊙O的半径即可;
(2)利用垂径定理得出OE⊥BC,∠OCE=45°,进而利用勾股定理得出即可;
(3)在AB上截取BF=BM,利用(1)中所求,得出∠ECP=135°,再利用全等三角形的判定与性质得出即可.
解:(1)如图1,连接OD,OC,
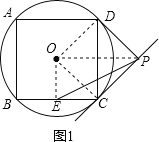
∵PC、PD是⊙O的两条切线,C、D为切点,
∴∠ODP=∠OCP=90°,
∵四边形ABCD是⊙O的内接正方形,
∴∠DOC=90°,OD=OC,
∴四边形DOCP是正方形,
∵AB=4,∠ODC=∠OCD=45°,
∴DO=CO=DCsin45°= ![]() ×4=2
×4=2 ![]() ;
;
(2)如图1,连接EO,OP,
∵点E是BC的中点,
∴OE⊥BC,∠OCE=45°,
则∠E0P=90°,
∴EO=EC=2,OP=![]() CO=4,
CO=4,
∴PE=![]() ;
;
(3)证明:如图2,在AB上截取BF=BM,
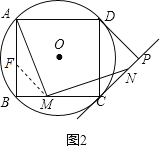
∵AB=BC,BF=BM,
∴AF=MC,∠BFM=∠BMF=45°,
∵∠AMN=90°,
∴∠AMF+∠NMC=45°,∠FAM+∠AMF=45°,
∴∠FAM=∠NMC,
∵由(1)得:PD=PC,∠DPC=90°,
∴∠DCP=45°,
∴∠MCN=135°,
∵∠AFM=180°-∠BFM=135°,
在△AFM和△CMN中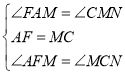
∴△AFM≌△CMN(ASA),
∴AM=MN.


科目:初中数学 来源: 题型:
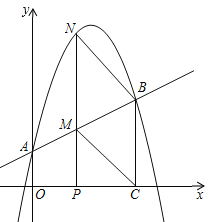
【题目】如图,抛物线![]() 与y轴交于A点,过点A的直线与抛物线交于另一点B,过点B作BC⊥x轴,垂足为点C(3,0).
与y轴交于A点,过点A的直线与抛物线交于另一点B,过点B作BC⊥x轴,垂足为点C(3,0).
(1)求直线AB的函数关系式;
(2)动点P在线段OC上从原点出发以每秒一个单位的速度向C移动,过点P作PN⊥x轴,交直线AB于点M,交抛物线于点N. 设点P移动的时间为t秒,MN的长度为s个单位,求s与t的函数关系式,并写出t的取值范围;
(3)设在(2)的条件下(不考虑点P与点O,点C重合的情况),连接CM,BN,当t为何值时,四边形BCMN为平行四边形?问对于所求的t值,平行四边形BCMN是否菱形?请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,直线CD与以线段OB为直径的半⊙A相切于点C,连接OC、BC,作OD⊥CD,垂足为D,OB=10,
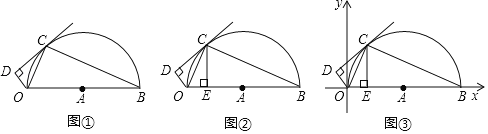
(1)求证:∠OCD=∠OBC;
(2)如图②,作CE⊥OB于点E,若CE=AE,求线段OD的长;
(3)如图③,在(2)的条件下,以O点为原点建立平面直角坐标系求△DOB外接圆的圆心坐标.
以下是优优和乐乐两位同学对第(3)小题的讨论
优优:这题很简单嘛,我只要求出这个三角形任意两条边的中垂线解析式,然后求交点坐标就行了.乐乐:我还有其他的好方法.
如果你是乐乐,你会怎么做?
查看答案和解析>>
科目:初中数学 来源: 题型:
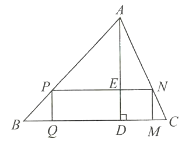
【题目】如图所示,![]() 是一块锐角三角形余料,边
是一块锐角三角形余料,边![]() 毫米,高
毫米,高![]() 毫米,要把它加工成一个矩形零件,使矩形的一边在
毫米,要把它加工成一个矩形零件,使矩形的一边在![]() 上,其余两个顶点分别在
上,其余两个顶点分别在![]() ,
,![]() 上,设该矩形的长
上,设该矩形的长![]() 毫米,宽
毫米,宽![]() 毫米.
毫米.
(1)求证:![]() ;
;
(2)当![]() 与
与![]() 分别取什么值时,矩形
分别取什么值时,矩形![]() 的面积最大?最大面积是多少?
的面积最大?最大面积是多少?
(3)当矩形![]() 的面积最大时,它的长和宽是关于
的面积最大时,它的长和宽是关于![]() 的一元二次方程
的一元二次方程![]() 的两个根,而
的两个根,而![]() ,
,![]() 的值又恰好分别是
的值又恰好分别是![]() ,10,12,13,
,10,12,13,![]() 这5个数据的众数与平均数,试求
这5个数据的众数与平均数,试求![]() 与
与![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
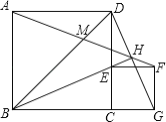
【题目】如图,![]() 、
、![]() 是正方形,
是正方形,![]() 在
在![]() 上,直线
上,直线![]() 、
、![]() 交于
交于![]() ,且
,且![]() ,
,![]() 、
、![]() 交于
交于![]() ,当
,当![]() 在线段
在线段![]() (不与
(不与![]() 、
、![]() 重合)上运动时,下列四个结论:①
重合)上运动时,下列四个结论:①![]() ;②
;②![]() 、
、![]() 所夹的锐角为
所夹的锐角为![]() ;③
;③![]() ;④若
;④若![]() 平分
平分![]() ,则正方形
,则正方形![]() 的面积为4,其中结论正确的是__(填序号)
的面积为4,其中结论正确的是__(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
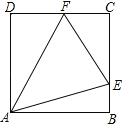
【题目】如图正方形ABCD,E、F分别为BC、CD边上一点.
(1)若∠EAF=45°,求证:EF=BE+DF;
(2)若该正方形ABCD的边长为1,如果△CEF的周长为2.求∠EAF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于二次函数y=2x2+4x-3,下列说法正确的是( )
A.图象与![]() 轴的交点坐标为
轴的交点坐标为![]()
B.图象的对称轴在![]() 轴的右侧
轴的右侧
C.当![]() 时,
时,![]() 的值随
的值随![]() 值的增大而减小
值的增大而减小
D.![]() 的最小值为-5
的最小值为-5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2-(m+2)x+(2m-1)=0。
(1)求证:方程恒有两个不相等的实数根;
(2)若此方程的一个根是1,请求出方程的另一个根,并求以此两根为边长的直角三角形的周长。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com