
【题目】如图①,正方形ABCD,点E,F分别在AB,CD上,DG⊥EF于点 H.
(1)求证:DG=EF;
(2)在图①的基础上连接AH,如图②,若 AH=AD,试确定DF与 CG的数量关系,并说明理由;
(3)在(2)的条件下,作∠FEK=45°,点 K在 BC边上,如图③,若AE=KG=2,求EK的长.

【答案】(1)证明见解析;(2)DF=2GC;(3)![]() .
.
【解析】
(1)过点F作FM⊥AB于点M,由题意可证MF=BC=CD,∠BEF=∠DFE=∠DGC,即可证△EFM≌△GDC,即可得EF=DG;
(2)过点A作AM⊥DG于点M,过点C作CN⊥DG于点N.由题意可证△ADM≌△DCN,可得DM=CN=![]() DH,由题意可证△DFH∽△DGC,可得
DH,由题意可证△DFH∽△DGC,可得![]() =2,即可得DF=2CG
=2,即可得DF=2CG
(3)过点F作FM⊥AB,连接MK,FK,由题意可证Rt△EMF≌Rt△GCD,可求EM=GC,由AM=DF=2GC,可得GC=EM=2,则可证点E,点F,点K,点M四点共圆,可得∠EMF=∠EKF=90°,可证△BEK≌△CKF,可得CK=BE=4,BM=2=BK,根据勾股定理可求EK的长.
(1)证明:过点F作FM⊥AB于点M,
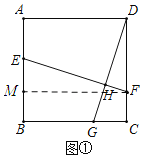
∵四边形ABCD是正方形,
∴∠B=∠C=90°,AB=BC=CD,AB∥CD
∵FM⊥AB,∠B=∠C=90°
∴四边形BCFM是矩形
∴MF=BC
即MF=CD
∵EF⊥DG,
∠C=90°
∴∠CDG+∠DGC=90°,∠CDG+∠DFE=90°
∴∠DGC=∠DFE
∵AB∥CD
∴∠BEF=∠EFD
∴∠BEF=∠DGC,且MF=CD,∠EMF=∠C=90°
∴△EFM≌△GDC(AAS)
∴EF=GD
(2)DF=2GC
过点A作AM⊥DG于点M,过点C作CN⊥DG于点N.
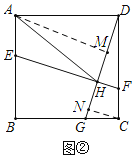
∵CN⊥DG,∠ADC=90°
∴∠ADG+∠GDC=90°,∠GDC+∠NCD=90°
∴∠ADG=∠DCN
∵AD=AH,AM⊥DG
∴MD=MH=![]() DH,
DH,
∵AD=CD,∠AMD=∠CND=90°,∠ADG=∠NCD
∴△ADM≌△DCN(AAS)
∴MD=NC
即DH=2NC
∵∠DGC=∠DFE,∠DHF=∠DCG=90°
∴△DFH∽△DGC
∴![]() =2
=2
∴DF=2GC
(3)如图:过点F作FM⊥AB,连接MK,FK,
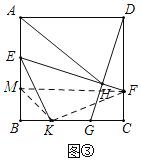
∵FM⊥AB,∠B=∠C=∠BAD=∠ADC=90°
∴四边形ADFM是矩形,四边形BCFM是矩形
∴DF=AM,AD=MF=BC=CD,
∵EF=DG,MF=CD
∴Rt△EMF≌Rt△GCD(HL)
∴GC=EM
∵DF=2GC
∴AM=2GC=2EM
∴AE=EM=2=CG
∴DF=4=CK
∴BK=BM
∴∠BMK=∠BKM=45°
∴∠FMK=45°
∵∠FMK=∠FEK=45°
∴点E,点F,点K,点M四点共圆
∴∠EMF=∠EKF=90°
∴∠FEK=∠EFK=45°
∴EK=FK,
∵∠BEK+∠EKB=90°,∠FKC+∠EKB=90°
∴∠FKC=∠BEK,且∠B=∠C=90°,EK=FK
∴△BEK≌△CKF(AAS)
∴CK=BE=4
∴BM=2=BK
∴EK=![]() .
.


科目:初中数学 来源: 题型:
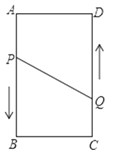
【题目】如图,A、B、C、D为矩形的四个顶点,AB=16cm,AD=6cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向点B移动,一直到达B为止,点Q以2 cm/s的速度向D移动.
(1)P、Q两点从出发开始到几秒?四边形PBCQ的面积为33cm2;
(2)P、Q两点从出发开始到几秒时?点P和点Q的距离是10cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2-4x+c的图象过点(-1, 0)和点(2,-9).
(1) 求该二次函数的解析式并写出其对称轴;
(2) 已知点P(2 , -2),连结OP , 在x轴上找一点M,使△OPM是等腰三角形,请直接写出点M的坐标(不写求解过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
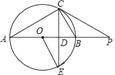
【题目】如图,已知,AB是⊙O的直径,点P在AB的延长线上,弦CE交AB于点,连结OE,AC,且∠P=∠E,∠POE=2∠CAB.
(1)求证:CE⊥AB;
(2)求证:PC是⊙O的切线;
(3)若BD=2OD,且PB=9,求⊙O的半径长和tan∠P的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
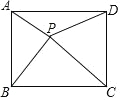
【题目】如图,点P是矩形ABCD内一点,连接PA、PB、PC、PD,已知AB=3,BC=4,设△PAB、△PBC、△PCD、△PDA的面积分别为S1、S2、S3、S4以下判断:①PA+PB+PC+PD的最小值为10;②若△PAB≌△PDC,则△PAD≌△PBC;③若S1=S2,则S3=S4;④若△PAB∽△PDA,则PA=2.4;其中正确的是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.若AE=1,则FM的长为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当m是何值时,关于x的方程(m2+2)x2+(m﹣1)x﹣4=3x2
(1)是一元二次方程;
(2)是一元一次方程;
(3)若x=﹣2是它的一个根,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习掷硬币的概率时,老师说:“掷一枚质地均匀的硬币,正面朝上的概率是![]() ”,小明做了下列三个模拟实验来验证.
”,小明做了下列三个模拟实验来验证.
①取一枚新硬币,在桌面上进行抛掷,计算正面朝上的次数与总次数的比值;
②把一个质地均匀的圆形转盘平均分成偶数份,并依次标上奇数和偶数,转动转盘,计算指针落在奇数区域的次数与总次数的比值;
③将一个圆形纸板放在水平的桌面上,纸板正中间放一个圆锥(如图),从圆锥的正上方往下撒米粒,计算其中一半纸板上的米粒数与纸板上总米粒数的比值. 上面的实验中,不科学的有( )
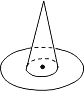
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com