
分析 (1)直接利用配方法求出二次函数的顶点式即可;
(2)利用(1)中所求得出二次函数的顶点坐标和对称轴;
(3)利用(1)中所求得出二次函数的最值.
解答 解:(1)y=$\frac{1}{2}$x2-3x+4
=$\frac{1}{2}$(x2-6x)+4
=$\frac{1}{2}$[(x-3)2-9]+4
=$\frac{1}{2}$(x-3)2-$\frac{1}{2}$;
(2)由(1)得:图象的顶点坐标为:(3,-$\frac{1}{2}$),
对称轴为:直线x=3;
(3)∵a=$\frac{1}{2}$>0,
∴函数的最小值为:-$\frac{1}{2}$.
点评 此题主要考查了配方法求二次函数的最值与顶点坐标,正确进行配方是解题关键.


 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:解答题
 我市出租车计费方法如图所示,x(千米)表示行驶里程,y(元)表示车费,请根据图象回答下列问题.
我市出租车计费方法如图所示,x(千米)表示行驶里程,y(元)表示车费,请根据图象回答下列问题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC是等边三角形,点E是AB的中点,延长CB至D,使BD=$\frac{1}{2}$BC.
如图,△ABC是等边三角形,点E是AB的中点,延长CB至D,使BD=$\frac{1}{2}$BC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (2,6) | B. | (1,1.5) | C. | (-1,1.5) | D. | (2,8) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
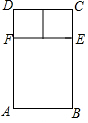 如图是一种窗框的设计示意图,矩形ABCD被分成上下两部分,上部的矩形CDFE由两个正方形组成,制作窗框的材料总长为6m.
如图是一种窗框的设计示意图,矩形ABCD被分成上下两部分,上部的矩形CDFE由两个正方形组成,制作窗框的材料总长为6m.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com