
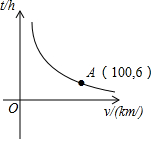
 一辆汽车从甲地开往乙地,随着汽车平均速度v(km/h)的变化,所需时间t(h)
一辆汽车从甲地开往乙地,随着汽车平均速度v(km/h)的变化,所需时间t(h) 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
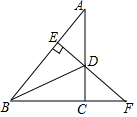 填空:把下面的推理过程补充完整,并在括号内注明理由.
填空:把下面的推理过程补充完整,并在括号内注明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 日期 | 10月1日 | 10月2日 | 10月3日 | 10月4日 | 10月5日 | 10月6日 | 10月7日 |
| 人数变化(万人) | +1.6 | +0.7 | +0.3 | -0.3 | -0.8 | +0.2 | -1.4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
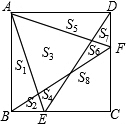 如图,正方形ABCD中,E、F分别是BC、CD边上的点,AE、DE、BF、AF把正方形分成8小块,各小块的面积分别为S1、S2、…S8,若S2=2,S7=3,S8=8,则S3的值为13.
如图,正方形ABCD中,E、F分别是BC、CD边上的点,AE、DE、BF、AF把正方形分成8小块,各小块的面积分别为S1、S2、…S8,若S2=2,S7=3,S8=8,则S3的值为13.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com