练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    17．圆锥的底面直径是6，母线长为5，则圆锥侧面展开图的圆心角是216度．

    分析 设圆锥侧面展开图的圆心角为n°，根据圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长和弧长公式得到6π=$\frac{n•π•5}{180}$，然后解方程即可．

    解答 解：设圆锥侧面展开图的圆心角为n°，
    所以6π=$\frac{n•π•5}{180}$，解得n=216．
    故答案为216．

    点评 本题考查了圆锥的计算：圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

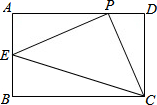    7．已知在矩形ABCD中，AB=2，BC=3，P是AD边上任意一点，（不含端点A、D），连接PC，过点P作PE⊥PC交AB于点E，在点P运动过程中，连接EC，是否存在∠ECP=∠DCP的情况？若存在，求出此时BE的长；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    8．△ABC的一边长为5，另两边分别是方程x2-6x+m=0的两根，则m的取值范围是（　　）
    A．m＞$\frac{11}{4}$B．$\frac{11}{4}$＜m≤9C．$\frac{11}{4}$≤m≤9D．m≤$\frac{11}{4}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．以下四个命题是真命题的是（　　）
    A．任意三点可以确定一个圆
    B．菱形对角线相等
    C．直角三角形斜边上的中线等于斜边的一半
    D．“打开电视机，中央一套正在直播巴西世界杯足球赛”是必然事件

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．一元二次方程2x2-3x-5=0的两个实数根分别为x1、x2，则x1+x2的值为（　　）
    A．$\frac{5}{2}$B．-$\frac{5}{2}$C．-$\frac{3}{2}$D．$\frac{3}{2}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．问题提出
    把多边形的任一边向两方延长，如果其它各边都在延长线的同一旁，则这样的多边形为凸多边形．如平行四边形、梯形等都是凸多边形．我们教材中所说的多边形如没作特别说明，一般都是指凸多边形．
    把多边形的某些边向两方延长，其他各边有不在延长所得直线的同一旁，这样的多边形叫做凹多边形．凹多边形会有哪些性质呢？
    初步认识
    如图（1），四边形ABCD中，延长BC到M，则边AB、CD分别在直线BM的两旁，所以四边形ABCD就是一个凹四边形．请你画一个凹五边形．（不要说明）
    性质探究
    请你完成凹四边形一个性质的证明：
    如图（2），在凹四边形ABCD中，求证：∠BCD=∠A+∠B+∠D．
    类比学习
    我们以前曾研究过凸四边形的中点四边形问题，如图（3），在四边形ABCD中，E、F、G、H分别是边AB、BC、CD、DA的中点，则四边形EFGH是平行四边形．当四边形ABCD满足一定条件时，四边形EFGH还可能是矩形、菱形或正方形．
    如图（4），在凹四边形ABCD中，AB=AD，CB=CD，E、F、G、H分别是边AB、BC、CD、DA的中点，请判断四边形EFGH的形状，并证明你的结论．
    拓展延伸
    如图（5），在凹四边形ABCD的边上求作一点P，使得∠BPD=∠A+∠B+∠D．（不写作法、证明，保留作图痕迹）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．小军家的玩具店进了一箱除颜色外都相同的塑料球共1000个，小军将箱中的球搅匀后，随机摸出一个球记下颜色，放回箱中；搅匀后再随机摸出一个球记下颜色，放回箱中；…多次重复上述实验后，发现摸到红球的频率逐渐稳定在0.2，由此可以估计纸箱内红球的个数约是200个．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．若二次函数y=ax2+bx+c（a＜0）的图象如图所示，且关于x的方程ax2+bx+c=k有两个不相等的实根，则常数k的取值范围是（　　）
    A．0＜k＜4B．-3＜k＜1C．k＜-3或k＞1D．k＜4

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．阅读材料：解方程组$\left\{\begin{array}{l}{x-y-1=0①}\\{4（x-y）-y=5②}\end{array}\right.$时，可由①得x-y=1③，然后再将③代入②得4×1-y=5，求得y=-1，从而进一步求得$\left\{\begin{array}{l}{x=0}\\{y=-1}\end{array}\right.$．这种方法被称为“整体代入法”．
    请用上述方法解方程组：$\left\{\begin{array}{l}{6x-2y=3}\\{（3x-y）（3x+4y）=6}\end{array}\right.$．

    查看答案和解析>>

    同步练习册答案