
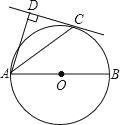
【题目】如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D.
(1)求证:AC平分∠DAB;
(2)过点O作线段AC的垂线OE,垂足为E(要求:尺规作图,保留作图痕迹,不写作法);
(3)若CD=4,AC=4![]() ,求垂线段OE的长.
,求垂线段OE的长.
【答案】(1)(2)见解析;(3)![]()
【解析】试题分析:(1)连接OC,由CD为圆O的切线,根据切线性质得到OC与CD垂直,又AD与CD垂直,根据平面上垂直于同一条直线的两直线平行得到AD与OC平行,由平行得一对内错角相等,又因为两半径OA与OC相等,根据等边对等角,得到一对相等的角,利用等量代换,即可得到∠DAC=∠OAC,即AC为∠DAB的平分线;
(2)以O为圆心,以大于O到AC的距离为半径画弧,与AC交于两点,分别以这两点为圆心,以大于这两点之间距离的一半长为半径在AC的另一侧画弧,两弧交于一点,经过此点与点O确定一条直线,即为所求的直线,如图所示;
(3)在直角三角形ACD中,由CD和AC的长,利用勾股定理求出AD的长,再根据垂径定理,由OE与AC 垂直,得到E为AC中点,求出AE的长,由(1)推出的角平分线得一对角相等,再由一对直角相等,根据两对对应角相等的两三角形相似,由相似得比例即可求出OE的长.
试题解析:(1)证明:连接OC.∵CD切⊙O于点C,∴OC⊥CD.又∵AD⊥CD,∴OC∥AD,∴∠OCA=∠DAC.∵OC=OA,∴∠OCA=∠OAC,∴∠OAC=∠DAC,∴AC平分∠DAB;
(2)解:点O作线段AC的垂线OE如图所示:
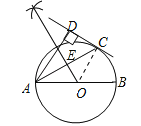
∴直线OE所求的直线;
(3)解:在Rt△ACD中,CD=4,AC=4![]() ,∴AD=
,∴AD=![]() =
=![]() =8.∵OE⊥AC,∴AE=
=8.∵OE⊥AC,∴AE=![]() AC=2
AC=2![]() .∵∠OAE=∠CAD,∠AEO=∠ADC,∴△AEO∽△ADC,∴
.∵∠OAE=∠CAD,∠AEO=∠ADC,∴△AEO∽△ADC,∴![]() =
=![]() ,∴OE=
,∴OE=![]() ×CD=
×CD=![]() ×4=
×4=![]() .即垂线段OE的长为
.即垂线段OE的长为![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】按照下列要求完成画图及相应的问题解答
(1)画直线![]() ;
;
(2)画![]() ;
;
(3)画线段![]() ;
;
(4)过![]() 点画直线
点画直线![]() 的垂线,交直线
的垂线,交直线![]() 于点
于点![]() ;
;
(5)请测量点![]() 到直线
到直线![]() 的距离为__________
的距离为__________![]() (精确到0.1
(精确到0.1 ![]() ) .
) .
查看答案和解析>>
科目:初中数学 来源: 题型:
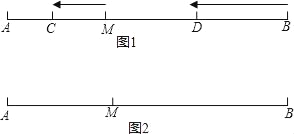
【题目】如图①,已知点M是线段AB上一点,点C在线段AM上,点D在线段BM上,C、D两点分别从M、B出发以1cm/s、3cm/s的速度沿直线BA向左运动,运动方向如箭头所示.
(1)若AB=10cm,当点C、D运动了2s,求AC+MD的值.
(2)若点C、D运动时,总有MD=3AC,则:AM= AB.
(3)如图②,若AM=![]() AB,点N是直线AB上一点,且AN﹣BN=MN,求
AB,点N是直线AB上一点,且AN﹣BN=MN,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果店在两周内,将标价为10元/斤的某种水果,经过两次降价后的价格为8.1元/斤,并且两次降价的百分率相同.
(1)求该种水果每次降价的百分率;
(2)从第一次降价的第1天算起,第x天(x为整数)的售价、销量及储存和损耗费用的相关信息如表所示.已知该种水果的进价为4.1元/斤,设销售该水果第x(天)的利润为y(元),求y与x(1≤x<15)之间的函数关系式,并求出第几天时销售利润最大?
时间x(天) | 1≤x<9 | 9≤x<15 | x≥15 |
售价(元/斤) | 第1次降价后的价格 | 第2次降价后的价格 | |
销量(斤) | 80﹣3x | 120﹣x | |
储存和损耗费用(元) | 40+3x | 3x2﹣64x+400 | |
(3)在(2)的条件下,若要使第15天的利润比(2)中最大利润最多少127.5元,则第15天在第14天的价格基础上最多可降多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某快递公司有甲、乙、丙三个机器人分配快件,甲单独完成需要x小时,乙单独完成需要y小时,丙单独完成需要z小时.
(1)求甲单独完成的时间是乙丙合作完成时间的几倍?
(2)若甲单独完成的时间是乙丙合作完成时间的a倍,乙单独完成的时间是甲丙合作完成时间的b倍,丙单独完成的时间是甲乙合作完成时间的c倍,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位急需用车,但又不准备买车,他们准备和一个体车主或一国营出租车公司其中的一家签订月租车合同.设汽车每月行驶xkm,应付给个体车主的月租费用是y1元,应付给出租公司的月租费用是y2元,y1、y2分别与x之间的函数关系图像(两条射线)如图所示,观察图像回答下列问题:
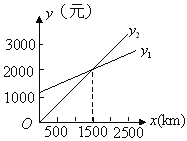
(1)每月行驶的路程在什么范围内时,租国有公司的车合算?
(2)每月行驶的路程等于多少时,租两家车的费用相同?
(3)如果这个单位估计每月行驶的路程为2300km,那么这个单位租哪家的车合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是正△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:①△BO′A可以由△BOC绕点B逆时针旋转60°得到;②点O与O′的距离为4;③∠AOB=150°;④S四边形AOBO![]() ;⑤S△AOC+S△AOB=
;⑤S△AOC+S△AOB=![]() .其中正确的结论是( )
.其中正确的结论是( )
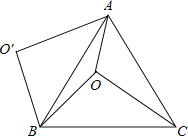
A.①②③⑤B.①②③④C.①②③④⑤D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面一段文字:
在数轴上点A,B分别表示数a,b.A,B两点间的距离可以用符号![]() 表示,利用有理数减法和绝对值可以计算A,B两点之间的距离
表示,利用有理数减法和绝对值可以计算A,B两点之间的距离![]() .
.
例如:当a=2,b=5时,![]() =5-2=3;当a=2,b=-5时,
=5-2=3;当a=2,b=-5时,![]() =
=![]() =7;当a=-2,b=-5时,
=7;当a=-2,b=-5时,![]() =
=![]() =3.综合上述过程,发现点A、B之间的距离
=3.综合上述过程,发现点A、B之间的距离![]() =
=![]() (也可以表示为
(也可以表示为![]() ).
).
请你根据上述材料,探究回答下列问题:
(1)数轴上表示1和3两点之间的距离是 ;
(2)表示数a和-2的两点间距离是6,则a= ;
(3)如果数轴上表示数a的点位于-4和3之间,求![]() 的值.
的值.
(4)是否存在数a,使代数式![]() 的值最小?若存在,请求出代数式的最小值,并直接写出数a的值或取值范围,若不存在,请简要说明理由.
的值最小?若存在,请求出代数式的最小值,并直接写出数a的值或取值范围,若不存在,请简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
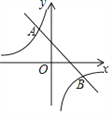
【题目】如图,一次函数y=k1x+b与反比例函数y=![]() 的图象交于点A(m,2),B(2,-1).
的图象交于点A(m,2),B(2,-1).
(1)求这两个函数的表达式;
(2)在x轴上是否存在点P(n,0),使△ABP为直角三角形,请你直接写出P点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com