
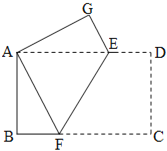
【题目】长方形具有四个内角均为直角,并且两组对边分别相等的特征.如图,把一张长方形纸片ABCD折叠,使点C与点A重合,折痕为EF.
(1)如果∠DEF=123°,求∠BAF的度数;
(2)判断△ABF和△AGE是否全等吗?请说明理由.
【答案】(1)∠BAF的度数为24°;(2)△ABF≌△AGE,理由见解析.
【解析】试题分析:(1)由∠DEF的度数以及AD∥BC可求出∠EFC的度数,因为翻折,所以∠AFE =∠EFC,不难求出∠AFB的度数,即可求出∠BAF的度数;(2)△ABF≌△AGE,由已知条件不难证明AB=AG,∠BAF=∠GAE,∠B=∠G,故可证明△ABF≌△AGE.
试题解析:
(1)∵四边形ABCD是长方形,
∴AB=CD,∠B=∠DAB=90°,AD∥BC.,
∴∠AEF=∠CFE,
∵∠DEF+∠AEF=180°,且∠DEF=123°,
∴∠AEF=57°,
∴∠CFE=57°,
∵四边形CDEF与四边形AGEF关于EF对称,
∴四边形CDEF≌四边形AGEF,
∴∠G=∠C=∠D=∠GAF=90°,AG=CD,∠AFE=∠CFE,
∴∠AFE=57°,
∵∠BFA+∠AFE+∠CFE=180°,
∴∠BFA=66°,
∵∠BFA+∠BAF=90°,
∴∠BAF=24°,
(2)△ABF≌△AGE,理由如下:
∵AG=CD,
∴AB=AG,
∵∠BAE=90°,∠GAF=90°,
∴∠BAE=∠GAF,
∴∠BAE-∠EAF=∠GAF-∠EAF,
∴∠BAF=∠GAE,
在△ABF和△AGE中,
 ,
,
∴△ABF≌△AGE(ASA).


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠A=60°,P为AB上一点, Q为BC延长线上一点,且PA=CQ,连PQ交AC边于D, PD=DQ,证明:△ABC为等边三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形![]() 中,
中,![]() 为正方形的外角
为正方形的外角![]() 的角平分线,点
的角平分线,点![]() 在线段
在线段![]() 上,过点
上,过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,交射线
,交射线![]() 于点
于点![]() .
.
(![]() )如图1,若点
)如图1,若点![]() 与点
与点![]() 重合.
重合.
①依题意补全图1.
②判断![]() 与
与![]() 的数量关系并加以证明.
的数量关系并加以证明.
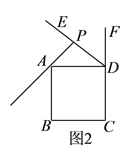
(![]() )如图2,若点
)如图2,若点![]() 恰好在线段
恰好在线段![]() 上,正方形
上,正方形![]() 的边长为
的边长为![]() ,请写出求
,请写出求![]() 长的思路(可以不写出计算结果).
长的思路(可以不写出计算结果).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程x2+(2m+1)x+m2﹣1=0有两个不相等的实数根.
(1)求m的取值范围;
(2)写出一个满足条件的m的值,并求此时方程的根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为满足市场需求,新生活超市在端午节前夕购进价格为3元/个的某品牌粽子,根据市场预测,该品牌粽子每个售价4元时,每天能出售500个,并且售价每上涨0.1元,其销售量将减少10个,为了维护消费者利益,物价部门规定,该品牌粽子售价不能超过进价的200%,请你利用所学知识帮助超市给该品牌粽子定价,使超市每天的销售利润为800元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接CD,且交OE于点F.
(1)求证:OE是CD的垂直平分线.
(2)若∠AOB=60,请你探究OE,EF之间有什么数量关系?并证明你的结论。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道“在同一平面内,经过直线外一点有且只有一条直线与已知直线平行”,

小伟同学想通过“同位角相等,两直线平行”作出图形,具体作法是,过点P任意作一条直线a与直线l相交,再以P为顶点作一个角,直线a为角的一边所在直线,则角的另一边所在直线与直线l平行.
(1)请你参照小伟同学的作法,帮他完成剩余的作图(保留作图痕迹,不写作法)
(2)你还有其它办法吗?请在备用图中完成(只需一种即可,保留作图痕迹,不写作法)


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com