
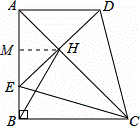
在四边形ABCD中,AD∥BC,∠ABC=90°,AB=BC,E为AB边上一点,∠BCE=15°,且AE=AD.连接DE交对角线AC于H,连接BH.下列结论正确的是 .(填番号)
①AC⊥DE;②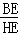 =
= ;③CD=2DH;④
;③CD=2DH;④ =
=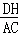 .
.
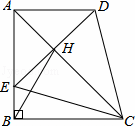
①③④
解:∵∠BAD=90°,AB=BC,
∴∠BAC=45°,
∴∠CAD=∠BAD﹣∠BAC=90°﹣45°=45°,
∴∠BAC=∠CAD,
∴∴AH⊥ED,
即AC⊥ED,故①正确;
∵△CHE为直角三角形,且∠HEC=60°
∴EC=2EH
∵∠ECB=15°,
∴EC≠4EB,
∴EH≠2EB;故②错误.
:∵∠BAD=90°,AB=BC,
∴∠BAC=45°,
∴∠CAD=∠BAD﹣∠BAC=90°﹣45°=45°,
∴∠BAC=∠CAD,
在△ACD和△ACE中,
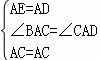 ,
,
∴△ACD≌△ACE(SAS),
∴CD=CE,
∵∠BCE=15°,
∴∠BEC=90°﹣∠BCE=90°﹣15°=75°,
∴∠CED=180°﹣∠BEC﹣∠AED=180°﹣75°﹣45°=60°,
∴△CDE为等边三角形,
∴∠DCH=30°,
∴CD=2DH,故③正确;
过H作HM⊥AB于M,
∴HM∥BC,
∴△AHM∽△ABC,
∴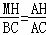 ,
,
∵DH=AH,
∴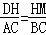 ,
,
∵△BEH和△CBE有公共底BE,
∴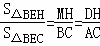 ,故④正确,
,故④正确,
故答案为:①③④.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
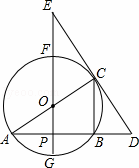
如图,⊙O中,FG、AC是直径,AB是弦,FG⊥AB,垂足为点P,过点C的直线交AB的延长线于点D,交GF的延长线于点E,已知AB=4,⊙O的半径为 .
.
(1)分别求出线段AP、CB的长;
(2)如果OE=5,求证:DE是⊙O的切线;
(3)如果tan∠E= ,求DE的长.
,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
已知抛物线y=x2﹣(k+2)x+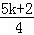 和直线y=(k+1)x+(k+1)2.
和直线y=(k+1)x+(k+1)2.
(1)求证:无论k取何实数值,抛物线总与x轴有两个不同的交点;
(2)抛物线于x轴交于点A、B,直线与x轴交于点C,设A、B、C三点的横坐标分别是x1、x2、x3,求x1•x2•x3的最大值;
(3)如果抛物线与x轴的交点A、B在原点的右边,直线与x轴的交点C在原点的左边,又抛物线、直线分别交y轴于点D、E,直线AD交直线CE于点G(如图),且CA•GE=CG•AB,求抛物线的解析式.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com