

���� ��1������$\left\{\begin{array}{l}{y=-\frac{1}{2}x+6}\\{y=x}\end{array}\right.$�����x��y��ֵ���Ƕ��٣����������C�������Ƕ��٣�
��2������ֱ�ǡ�FCE��ת�����У�tan��CED��ֵ���䣮���ȹ���C��CG��x���ڵ�G������C��CH��y���ڵ�H�����ݡ�DCH+��DCG=90�㣬��ECG+��DCG=90�㣬�Ƶá�DCH=��ECG��Ȼ�����ȫ���������ж��ķ������жϳ���CDH�ա�CEG���Ƶ�CD=CE������tan��CED=$\frac{CD}{CE}$=1���ݴ˽�ɣ�
����ֱ�ǡ�FCE��ת�����У�������C��E��FΪ��������������ODE���ƣ��������⣬�����������������ODE�ס�CEF��������ODE�ס�CFE��Ȼ��������������ε����ʣ��������ۣ������D��������Ƕ��ټ��ɣ�
��� �⣺��1������$\left\{\begin{array}{l}{y=-\frac{1}{2}x+6}\\{y=x}\end{array}\right.$
���$\left\{\begin{array}{l}{x=4}\\{y=4}\end{array}\right.$
���C�������ǣ�4��4����
��2������ֱ�ǡ�FCE��ת�����У�tan��CED��ֵ���䣮
��ͼ1������C��CG��x���ڵ�G������C��CH��y���ڵ�H�� ��
��
�ߡ�DCH+��DCG=90�㣬��ECG+��DCG=90�㣬
���DCH=��ECG��
�ڡ�CDH�ա�CEG�У�
$\left\{\begin{array}{l}{��DCH=��ECG}\\{CH=CG=4}\\{��CHD=��CGE=90��}\end{array}\right.$��
���CDH�ա�CEG��
��CD=CE��
����Rt��CDE��tan��CED=$\frac{CD}{CE}$=1��
����ֱ�ǡ�FCE��ת�����У�tan��CED��ֵ���䣬�����1��
����ֱ�ǡ�FCE��ת�����У�������C��E��FΪ��������������ODE���ƣ�
����ͼ2�� ��
��
����ODE�ס�CEF��
���OED=��CFE��
��DE=DF��
�֡�OD��EF��
��OE=OF��
�ߡ�FCE=90�㣬
���O��Rt��CEFб��EF���е㣬
��$OC=\frac{1}{2}EF$��
��CG=CH=4��
��OC=$4\sqrt{2}$��
��$OE=OF=OC=4\sqrt{2}$��
��CH��EF��
���CHD�ס�FOD��
��$\frac{HD}{OD}=\frac{CH}{FO}$��
��$\frac{4-OD}{OD}=\frac{4}{{4\sqrt{2}}}$��
���$OD=8-4\sqrt{2}$��
��D��0��8-4$\sqrt{2}$����
����ͼ3������C��CM��y���ڵ�M������C��CN��x���ڵ�N�� ��
��
����ODE�ס�CFE��
���OED=��CEF��
�ߵ�C�������ǣ�4��4����
��CM=CN=4��
��Rt��CMD��Rt��CNE��
$\left\{\begin{array}{l}{CD=CE}\\{CM=CN}\end{array}\right.$��
���CMD�ա�CNE��HL����
���CDM=��CE0��
�ɢ٣��ɵá�CDEΪ����ֱ�������Σ�
���CED=45�㣬
���CEO=��OED=��CDM=22.5�㣬
��CM=CN=4��
���CMOΪ����ֱ�������Σ�
���COM=45�㣬
���OCD=��COM-��CDM=45��-22.5��=22.5�㣬
���OCD=��ODC��
��OD=OC��
��CM=CN=4��
��OC=4$\sqrt{2}$��
��OD=OC=4$\sqrt{2}$��
�ߵ�D��y�Ḻ�����ϣ�
��D��0��-4$\sqrt{2}$����
���ϣ��ɵ�
��ֱ�ǡ�FCE��ת�����У�������C��E��FΪ��������������ODE���ƣ���D������Ϊ��0��8-4$\sqrt{2}$����0��-4$\sqrt{2}$����
���� ��1��������Ҫ�����˼��α任�ۺ��⣬�����˷������������������˷�������˼���Ӧ�ã����������ν��˼���Ӧ�ã�Ҫ�������գ�
��2�����������ȫ�������ε��ж������ʵ�Ӧ�ã�Ҫ�������գ�������Ĺؼ���Ҫ��ȷ�����ж�����1��SSS--�����߷ֱ��Ӧ��ȵ�����������ȫ�ȣ����ж�����2��SAS--������нǷֱ��Ӧ��ȵ�����������ȫ�ȣ����ж�����3��ASA--���Ǽ���б߷ֱ��Ӧ��ȵ�����������ȫ�ȣ����ж�����4��AAS--���Ǽ�����һ���ǵĶԱ߶�Ӧ��ȵ�����������ȫ�ȣ����ж�����5��HL--б����ֱ�DZ߶�Ӧ��ȵ�����ֱ��������ȫ�ȣ�
��3��������������������Ƶ��ж������ʵ�Ӧ�ã�Ҫ�������գ�������Ĺؼ���Ҫ��ȷ�������߷��������Ӧ�ߵı���ȵ��������������ƣ���������нǷ��������Ӧ�ߵı�����ҼнǶ�Ӧ��ȵ��������������ƣ������Ƿ���������Ƕ�Ӧ��ȵ��������������ƣ�


 ������������Ӧ����ϵ�д�
������������Ӧ����ϵ�д� ͬ����չ�Ķ�ϵ�д�
ͬ����չ�Ķ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
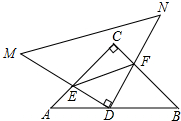 ��ͼ������������ֱ����������ͼ�ڷţ�DΪAB�ߵ��е㣬E��F�ֱ�����AC��BC�ϣ����ڶ˵㣩������MND����D����תʱ����DE+DF=x��AB=10����CEF�����Ϊy����y��x֮��ĺ�����ͼ�����Ϊ��������
��ͼ������������ֱ����������ͼ�ڷţ�DΪAB�ߵ��е㣬E��F�ֱ�����AC��BC�ϣ����ڶ˵㣩������MND����D����תʱ����DE+DF=x��AB=10����CEF�����Ϊy����y��x֮��ĺ�����ͼ�����Ϊ��������| A�� | 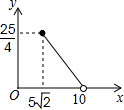 | B�� | 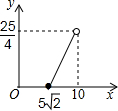 | C�� | 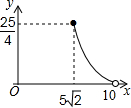 | D�� | 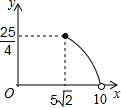 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
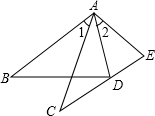 ��ͼ���ڡ�ABD�͡�ACE�У�AB=AC��������������ʽ��
��ͼ���ڡ�ABD�͡�ACE�У�AB=AC��������������ʽ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
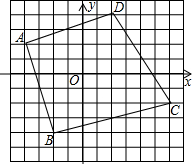 ��֪����ͼ���ı���ABCD�Ķ�������ֱ�ΪA��-4��2����B��-2��-4����C��6��-2����D��2��4��������O��Ϊλ���������ı���A��B��C��D�䣬ʹ�ı���ABCD���ı���A��B��C��D���λ�Ʊ�Ϊ2��1��ֻ��һ���������
��֪����ͼ���ı���ABCD�Ķ�������ֱ�ΪA��-4��2����B��-2��-4����C��6��-2����D��2��4��������O��Ϊλ���������ı���A��B��C��D�䣬ʹ�ı���ABCD���ı���A��B��C��D���λ�Ʊ�Ϊ2��1��ֻ��һ����������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
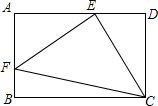 ��ͼ������ABCD���ܳ���16��DE=2����FEC�ǵ��������Σ���FEC=90�㣬��AE�ij��ǣ�������
��ͼ������ABCD���ܳ���16��DE=2����FEC�ǵ��������Σ���FEC=90�㣬��AE�ij��ǣ�������| A�� | 3 | B�� | 4 | C�� | 5 | D�� | 6 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com