
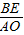 =
=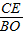 =
=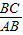 =
= ,BE=
,BE= AO=3,CE=
AO=3,CE= OB=
OB= 故点C的坐标为(t+3,
故点C的坐标为(t+3, ).由于AB⊥BC,AB=2BC,∴S△ABC=
).由于AB⊥BC,AB=2BC,∴S△ABC= AB•BC=BC2.在Rt△ABC中,由勾股定理得BC2=CE2+BE2=
AB•BC=BC2.在Rt△ABC中,由勾股定理得BC2=CE2+BE2= t2+9,即S△ABC=
t2+9,即S△ABC= t2+9.
t2+9.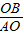 =
=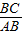 =
= ,即
,即 =
= ,∴t=3,即B(3,0).
,∴t=3,即B(3,0). CG,由△AOB∽△GEB,
CG,由△AOB∽△GEB,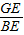 =
=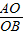 ,故GE=
,故GE=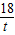 .由于HE=AO=6,CE=
.由于HE=AO=6,CE= ,t2-24t-36=0,解得:t=12±6
,t2-24t-36=0,解得:t=12±6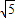 .因为t≥0,所以t=12+6
.因为t≥0,所以t=12+6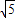 ,即B(12+6
,即B(12+6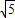 ,0).
,0). ),
), ,由BD∥y轴,AB=AD得,∠BAO=∠ABD,∠FAC=∠BDA,∠ABD=∠ADB故∠BAO=∠FAC,
,由BD∥y轴,AB=AD得,∠BAO=∠ABD,∠FAC=∠BDA,∠ABD=∠ADB故∠BAO=∠FAC,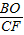 =
=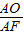 ,求得t的关系式t2-24t-36=0,解得:t=12±6
,求得t的关系式t2-24t-36=0,解得:t=12±6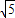 .因为-3≤t<0,所以t=12-6
.因为-3≤t<0,所以t=12-6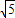 ,即B(12-6
,即B(12-6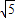 ,0).
,0). ),故CF=-(t+3),AF=6-
),故CF=-(t+3),AF=6- ,由于AB=BD,故∠D=∠BAD.又因为BD∥y轴,故∠D=∠CAF,∠BAC=∠CAF.又因为∠ABC=∠AFC=90°,AC=AC,所以△ABC≌△AFC,故AF=AB,CF=BC,∴AF=2CF,即6-
,由于AB=BD,故∠D=∠BAD.又因为BD∥y轴,故∠D=∠CAF,∠BAC=∠CAF.又因为∠ABC=∠AFC=90°,AC=AC,所以△ABC≌△AFC,故AF=AB,CF=BC,∴AF=2CF,即6- =-2(t+3),解得:t=-8,即B(-8,0).
=-2(t+3),解得:t=-8,即B(-8,0).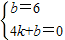 ,
,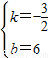 ,
, x+6.
x+6.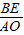 =
=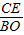 =
=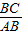 =
= ,
, AO=3,CE=
AO=3,CE= OB=
OB= ,
, ).
). OE•(AO+EC)=
OE•(AO+EC)= (t+3)(6+
(t+3)(6+ )=
)= t2+
t2+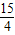 t+9,
t+9, AO•OB=
AO•OB= ×6•t=3t,
×6•t=3t, BE•CE=
BE•CE= ×3×
×3× =
= t,
t, t2+
t2+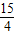 t+9-3t-
t+9-3t- t
t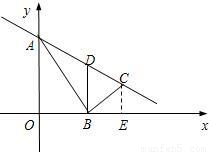
 t2+9.
t2+9. AB•BC=BC2.
AB•BC=BC2. t2+9,
t2+9, t2+9.
t2+9.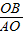 =
=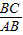 =
= ,
, =
= ,
,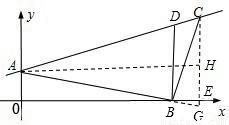 过点A画AH⊥CG于H.
过点A画AH⊥CG于H. CG,
CG,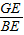 =
=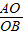 ,
,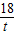 .
. ,
,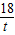 +6=
+6= ×(
×( +
+ ),
),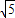 .因为t≥0,
.因为t≥0,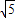 ,即B(12+6
,即B(12+6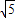 ,0).
,0).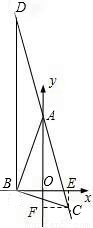 ②当-3≤t<0时,如图,∠DAB是钝角.设AD=AB
②当-3≤t<0时,如图,∠DAB是钝角.设AD=AB ),
), ,
,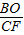 =
=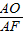 ,
,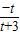 =
=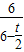 ,
,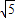 .因为-3≤t<0,
.因为-3≤t<0,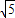 ,即B(12-6
,即B(12-6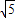 ,0).
,0).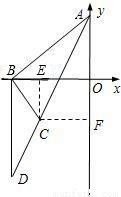 ③当t<-3时,如图,∠ABD是钝角.设AB=BD,
③当t<-3时,如图,∠ABD是钝角.设AB=BD, ),
), ,
, =-2(t+3),
=-2(t+3),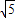 ,0),B3(12-6
,0),B3(12-6 ,0),B4(-8,0).
,0),B4(-8,0).

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2011年3月黑龙江省大庆市第六十三中学月考数学试卷(解析版) 题型:解答题
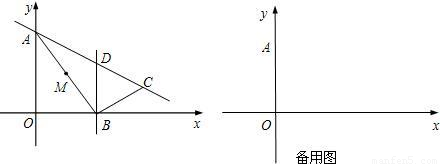
 图象与BC交于点D,与AB交于点E,其中D(1,3).
图象与BC交于点D,与AB交于点E,其中D(1,3).
查看答案和解析>>
科目:初中数学 来源:2009年全国中考数学试题汇编《图形的相似》(06)(解析版) 题型:解答题
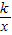 图象与BC交于点D,与AB交于点E,其中D(1,3).
图象与BC交于点D,与AB交于点E,其中D(1,3).
查看答案和解析>>
科目:初中数学 来源:2009年全国中考数学试题汇编《四边形》(11)(解析版) 题型:解答题
 图象与BC交于点D,与AB交于点E,其中D(1,3).
图象与BC交于点D,与AB交于点E,其中D(1,3).
查看答案和解析>>
科目:初中数学 来源:2009年全国中考数学试题汇编《反比例函数》(05)(解析版) 题型:解答题
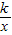 图象与BC交于点D,与AB交于点E,其中D(1,3).
图象与BC交于点D,与AB交于点E,其中D(1,3).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com