
分析 (1)先把-4移项,再利用配方法解方程即可;
(2)把点(2,-4)代入y=x2-2mx+4即可得出m的值,再把m的值代入二次函数y=x2-2mx+4中,令y=-1即可得出答案.
解答 解:(1)移项得,x2-2x=4
配方得,x2-2x+1=5,
即(x-1)2=5,
∴x-1=±$\sqrt{5}$,
∴x1=1+$\sqrt{5}$,x2=1-$\sqrt{5}$;
(2)把点(2,-4)代入y=x2-2mx+4,得4-4m+4=-4,
解得m=3,
把m=3代入y=x2-2mx+4得y=x2-6x+4,
令y=-1得x2-6x+4=-1,
解得,x1=1,x2=5.
点评 本题考查了二次函数图象上点的坐标特征以及解一元二次方程,掌握点在图象上和点满足解析式,以及一元二次方程的解法是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
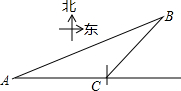 钓鱼岛是我国的神圣领土,中国人民维护国家领土完整的决心是坚定的,多年来,我国的海监、渔政等执法船定期开赴钓鱼岛巡视.某日,我海监船(A处)测得钓鱼岛(B处)距离为20海里,海监船继续向东航行,在C处测得钓鱼岛在北偏东45°的方向上,距离为10$\sqrt{2}$海里,求AC的距离.(结果保留根号)
钓鱼岛是我国的神圣领土,中国人民维护国家领土完整的决心是坚定的,多年来,我国的海监、渔政等执法船定期开赴钓鱼岛巡视.某日,我海监船(A处)测得钓鱼岛(B处)距离为20海里,海监船继续向东航行,在C处测得钓鱼岛在北偏东45°的方向上,距离为10$\sqrt{2}$海里,求AC的距离.(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,路灯(P点)距地面8米,身高1.6米的小明从距离路灯的底部(O点)20米的A点,沿OA所在的直线行走14米到B点(B点在A点的左边)时,身影的长度是变长了还是变短了?变长或变短了多少米?
如图,路灯(P点)距地面8米,身高1.6米的小明从距离路灯的底部(O点)20米的A点,沿OA所在的直线行走14米到B点(B点在A点的左边)时,身影的长度是变长了还是变短了?变长或变短了多少米?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在△ABC中(AB<BC),在BC上截取BD=BA,作∠ABC的平分线与AD相交于点P,连接PC,若△ABC的面积为3,则△BPC的面积为$\frac{3}{2}$.
如图,在△ABC中(AB<BC),在BC上截取BD=BA,作∠ABC的平分线与AD相交于点P,连接PC,若△ABC的面积为3,则△BPC的面积为$\frac{3}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com