

分析 (1)利用相似三角形的性质求得EF于DF的比值,依据△CEF和△CDF同高,则面积的比就是EF与DF的比值,据此即可求解;
(2)利用相似三角形的对应边成比例,得出$\frac{AF}{AC}$=$\frac{m+1}{m+2}$,再根据AC=2OA,即可得出结论;
(3)依据相似三角形的对应边成比例,可得$\frac{EF}{DF}$=$\frac{CF}{AF}$=$\frac{CE}{AD}$=$\frac{1}{m+1}$,再根据FG∥CD,得出$\frac{EG}{CG}$=$\frac{EF}{DF}$=$\frac{1}{m+1}$,根据FG∥AB,得出$\frac{CG}{BG}$=$\frac{CF}{AF}$=$\frac{1}{m+1}$,两式相乘即可得到$\frac{EG}{BG}$=($\frac{1}{m+1}$)2.
解答  解:(1)∵$\frac{CE}{EB}$=$\frac{1}{3}$,
解:(1)∵$\frac{CE}{EB}$=$\frac{1}{3}$,
∴$\frac{CE}{BC}$=$\frac{1}{4}$,
∵四边形ABCD是矩形,
∴AD∥BC,AD=BC,
∴△CEF∽△ADF,
∴$\frac{EF}{DF}$=$\frac{CE}{AD}$,
∴$\frac{EF}{DF}$=$\frac{CE}{BC}$=$\frac{1}{4}$,
∴$\frac{{S}_{△CEF}}{{S}_{△CDF}}$=$\frac{EF}{DF}$=$\frac{1}{4}$;
(2)设EC=1,则BE=m,
∵四边形ABCD是矩形,
∴AD∥BC,AD=BC=m+1,
∴△CEF∽△ADF,
∴$\frac{CF}{AF}$=$\frac{CE}{AD}$=$\frac{1}{m+1}$,
∴$\frac{AF}{AC}$=$\frac{m+1}{m+2}$,
∵$\frac{OA}{AC}$=$\frac{1}{2}$,
∴AC=2OA,
∴$\frac{AF}{2OA}$=$\frac{m+1}{m+2}$,
∴$\frac{AF}{OA}$=$\frac{2m+2}{m+2}$;
(3)结论:$\frac{EG}{BG}$=($\frac{1}{m+1}$)2,理由如下:
设EC=1,则BE=m,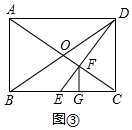
∵四边形ABCD是矩形,
∴AD∥BC,AD=BC=m+1,
∴△CEF∽△ADF,
∴$\frac{EF}{DF}$=$\frac{CF}{AF}$=$\frac{CE}{AD}$=$\frac{1}{m+1}$,
∵FG⊥BC,
∴FG∥CD,
∴$\frac{EG}{CG}$=$\frac{EF}{DF}$=$\frac{1}{m+1}$,①
∵FG∥AB,
∴$\frac{CG}{BG}$=$\frac{CF}{AF}$=$\frac{1}{m+1}$,②
由①×②,可得$\frac{EG}{CG}$×$\frac{CG}{BG}$=$\frac{1}{m+1}$×$\frac{1}{m+1}$,
即$\frac{EG}{BG}$=($\frac{1}{m+1}$)2.
点评 本题属于相似形综合题,主要考查了相似三角形的判定与性质,矩形的性质以及平行线分线段成比例定理的综合应用,解决问题的关键是依据相似三角形对应边成比例列式计算.第(3)问的难点在于综合运用相似三角形的性质以及平行线分线段成比例定理.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:选择题
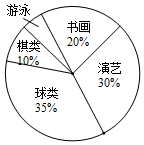 如图是某校参加各兴趣小组的学生人数分布扇形统计图,若参加人数最多的小组是70人,则参加人数最少的小组有( )
如图是某校参加各兴趣小组的学生人数分布扇形统计图,若参加人数最多的小组是70人,则参加人数最少的小组有( )| A. | 5人 | B. | 10人 | C. | 20人 | D. | 40人 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系xOy中,抛物线y=mx2-2mx+2(m≠0)与y轴交于点A,其对称轴与x轴交于点B.
在平面直角坐标系xOy中,抛物线y=mx2-2mx+2(m≠0)与y轴交于点A,其对称轴与x轴交于点B.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系xOy中,抛物线y=x2-2mx+m2-1与x轴交于A,B两点(点A在点B左侧)
在平面直角坐标系xOy中,抛物线y=x2-2mx+m2-1与x轴交于A,B两点(点A在点B左侧)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解商丘市的空气质量情况 | B. | 了解包河的水污染情况 | ||
| C. | 了解商丘市居民的环保意识 | D. | 了解全班同学每周体育锻炼的时间 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 中位数是10 | B. | 众数是10 | C. | 平均数是9.5 | D. | 方差是16 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com