
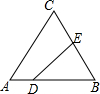
 如图,在△ABC中,AC=BC=25,AB=30,D是AB上的一点(不与A、B重合),DE⊥BC,垂足是点E,设BD=x,四边形ACED的周长为y,则下列图象能大致反映y与x之间的函数关系的是( )
如图,在△ABC中,AC=BC=25,AB=30,D是AB上的一点(不与A、B重合),DE⊥BC,垂足是点E,设BD=x,四边形ACED的周长为y,则下列图象能大致反映y与x之间的函数关系的是( )| A. | 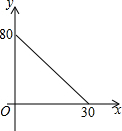 | B. |  | C. | 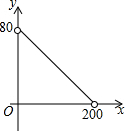 | D. | 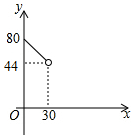 |
分析 由△DEB∽△CMB,得$\frac{BD}{BC}$=$\frac{DE}{CM}$=$\frac{EB}{BM}$,求出DE、EB,即可解决问题.
解答 解:如图,作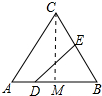 CM⊥AB于M.
CM⊥AB于M.
∵CA=CB,AB=30,CM⊥AB,
∴AM=BM=15,CM=$\sqrt{A{C}^{2}-B{M}^{2}}$=20
∵DE⊥BC,
∴∠DEB=∠CMB=90°,
∵∠B=∠B,
∴△DEB∽△CMB,
∴$\frac{BD}{BC}$=$\frac{DE}{CM}$=$\frac{EB}{BM}$,
∴$\frac{x}{25}$=$\frac{DE}{20}$=$\frac{EB}{15}$,
∴DE=$\frac{4}{5}x$,EB=$\frac{3}{5}x$,
∴四边形ACED的周长为y=25+(25-$\frac{3}{5}x$)+$\frac{4}{5}x$+30-x=-$\frac{4}{5}$x+80.
∵0<x<30,
∴图象是B.
故选B.
点评 本题考查函数图象、等腰三角形的性质、相似三角形的判定和性质等知识,解题的关键是构建函数关系式,注意自变量的取值范围,属于中考常考题型.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{19}{2}$ | B. | $\frac{21}{2}$ | C. | 7 | D. | 13 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3.036×103 | B. | 3.036×1011 | C. | 3036×108 | D. | 0.3036×1012 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
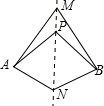 如图,直线MN是四边形AMBN的对称轴,点P是直线MN上的点,下列判断错误的是( )
如图,直线MN是四边形AMBN的对称轴,点P是直线MN上的点,下列判断错误的是( )| A. | AM=BM | B. | AP=BN | C. | ∠MAP=∠MBP | D. | ∠ANM=∠BNM |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,△AOB中,∠O=90°,AO=8cm,BO=6cm,点C从A点出发,在边AO上以2cm/s的速度向O点运动,与此同时,点D从点B出发,在边BO上以1.5cm/s的速度向O点运动,过OC的中点E作CD的垂线EF,则当点C运动了$\frac{17}{8}$s时,以C点为圆心,1.5cm为半径的圆与直线EF相切.
如图,△AOB中,∠O=90°,AO=8cm,BO=6cm,点C从A点出发,在边AO上以2cm/s的速度向O点运动,与此同时,点D从点B出发,在边BO上以1.5cm/s的速度向O点运动,过OC的中点E作CD的垂线EF,则当点C运动了$\frac{17}{8}$s时,以C点为圆心,1.5cm为半径的圆与直线EF相切.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com