
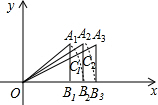
 如图,在平面直角坐标系中,已知A1(1,1),B1(1,0),以O为圆心OA1为半径作圆弧交x轴于B2,作Rt△A2B2O使得A2B2=A1B1且OA2交A1B1于C1,以O为圆心OA2为半径作圆弧交x轴于B3,作Rt△A3B3O使得A3B3=A2B2且OA3交A2B2于C2,…,按此规律,则Cn的纵坐标为($\sqrt{n}$,$\frac{\sqrt{n}}{\sqrt{n+1}}$)(结果用n的代数式表示)
如图,在平面直角坐标系中,已知A1(1,1),B1(1,0),以O为圆心OA1为半径作圆弧交x轴于B2,作Rt△A2B2O使得A2B2=A1B1且OA2交A1B1于C1,以O为圆心OA2为半径作圆弧交x轴于B3,作Rt△A3B3O使得A3B3=A2B2且OA3交A2B2于C2,…,按此规律,则Cn的纵坐标为($\sqrt{n}$,$\frac{\sqrt{n}}{\sqrt{n+1}}$)(结果用n的代数式表示) 分析 易证Rt△OC1 B1∽Rt△OA2 B2,所以有$\frac{{C}_{1}B}{{A}_{2}{B}_{2}}=\frac{OB1}{O{B}_{2}}$,而A2 B2=1,OB1=1,OB2=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$.所以C1 B1=$\frac{1×1}{\sqrt{2}}$,故:C1(1,$\frac{1}{\sqrt{2}}$)…以此类推,直至找出规律.
解答 解:由题意得:Rt△OC1 B1∽Rt△OA2 B2,
∴$\frac{{C}_{1}B}{{A}_{2}{B}_{2}}=\frac{OB1}{O{B}_{2}}$
∵A2 B2=1,OB1=1,OB2=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,
∴C1 B1=$\frac{1×1}{\sqrt{2}}$,C1 (1,$\frac{1}{\sqrt{2}}$).
同理可得:C2 B2=$\frac{1×\sqrt{2}}{\sqrt{3}}$,C2 ($\sqrt{2}$,$\frac{1×\sqrt{2}}{\sqrt{3}}$)
C3 B3=$\frac{1×\sqrt{3}}{\sqrt{4}}$,C3 ($\sqrt{3}$,$\frac{1×\sqrt{3}}{\sqrt{4}}$)…
∴Cn ($\sqrt{n}$,$\frac{\sqrt{n}}{\sqrt{n+1}}$)
点评 本题考查了直角坐标系中点的坐标的变化规律问题,解题的关键是求出Cn Bn的长与OBn 的长.


科目:初中数学 来源: 题型:填空题
 如图,圆锥的底面半径是2cm,当圆锥的高由小到大变化时,圆锥的体积也随之发生了变化.在这个变化过程中,自变量是圆锥的高,因变量是圆锥的体积.
如图,圆锥的底面半径是2cm,当圆锥的高由小到大变化时,圆锥的体积也随之发生了变化.在这个变化过程中,自变量是圆锥的高,因变量是圆锥的体积.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 数量(千克) | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | … |
| 售价(元) | 1.5 | 3 | 4.5 | 6 | 7.5 | 9 | 10.5 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,是反映了爷爷每天晚饭后从家中出发去散步的时间与距离之间的关系的一幅图.
如图所示,是反映了爷爷每天晚饭后从家中出发去散步的时间与距离之间的关系的一幅图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某中学九(2)班同学为了了解2014年某小区家庭月均用水情况,随机调查了该小区的部分家庭,并将调查数据进行如下整理:
某中学九(2)班同学为了了解2014年某小区家庭月均用水情况,随机调查了该小区的部分家庭,并将调查数据进行如下整理:| 月均用水量x(吨) | 频数 | 频率 |
| 0<x≤5 | 6 | 0.12 |
| 5<x≤10 | 12 | 0.24 |
| 10<x≤15 | 16 | 0.32 |
| 15<x≤20 | 10 | 0.20 |
| 20<x≤25 | 4 | 0.08 |
| 25<x≤3 | 2 | 0.04 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com