
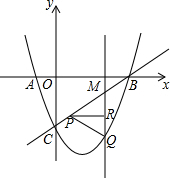
 如图,抛物线y=ax2-(a+1)x-3与x轴交于点A、B,与y轴交于点C,∠BCO=45°,点M为线段BC上异于B、C的一动点,过点M与y轴平行的直线交抛物线于点Q,点R为线段QM上一动点,RP⊥QM交直线BC于点P.设点M的横坐标为m.
如图,抛物线y=ax2-(a+1)x-3与x轴交于点A、B,与y轴交于点C,∠BCO=45°,点M为线段BC上异于B、C的一动点,过点M与y轴平行的直线交抛物线于点Q,点R为线段QM上一动点,RP⊥QM交直线BC于点P.设点M的横坐标为m.分析 (1)可先求得C点坐标,利用∠BCO=45°可求得B点坐标,代入抛物线解析式可求得a,可求得抛物线解析式;
(2)可先求得Q的坐标,利用待定系数法可求得直线BC解析式,设出P点坐标,则可表示出PR、QR的长,由等腰三角形的性质可得到关于P点坐标的方程,可求得P点坐标;
(3)①由题意可知PR=RM,故PR+QR=MQ,设出可用m表示出Q点坐标,则可表示出MQ的长,利用二次函数的性质可求得其最大值;②用PR表示出△PQR的面积,利用二次函数的性质可求得其最大值.
解答  解:
解:
(1)在y=ax2-(a+1)x-3中,令x=0可得y=-3,
∴C(0,-3),即OC=3,
∵∠BCO=45°,
∴OB=OC=3,
∴B(3,0),
把B点坐标代入抛物线解析式可得9a-3(a+1)-3=0,求得a=1,
∴抛物线的表达式为y=x2-2x-3;
(2)当m=2时,则M(2,0),
把x=2代入抛物线解析式可得y=-3,
∴Q(2,-3),
∵B(3,0),C(0,-3),
∴直线BC表达式为y=x-3,
∴可设P(p,p-3),则PR=2-p,QR=p-3-(-3)=p,
∵PR=QR,
∴2-p=p,解得p=1,
∴P(1,-2);
(3)①由(2)可知M(m,m-3),Q(m,m2-2m-3),
∵PR⊥MQ,
∴∠MPR=45°,
∴MR=PR,
∴PR+QR=PR+MR=QM=m-3-(m2-2m-3)=-m2+3m=-(m-$\frac{3}{2}$)2+$\frac{9}{4}$,
∵-1<0,
∴当m=$\frac{3}{2}$时,PR+QR取最大值$\frac{9}{4}$;
②∵PR+QR的最大值为$\frac{9}{4}$,
∴S△PQR=$\frac{1}{2}$PR•QR≤$\frac{1}{2}$PR($\frac{9}{4}$-PR)=-$\frac{1}{2}$(PR-$\frac{9}{8}$)2+$\frac{81}{128}$,
∵$\frac{1}{2}$<0,
∴当PR=$\frac{9}{8}$时,△PQR的面积取得最大值$\frac{81}{128}$.
点评 本题为二次函数的综合应用,涉及待定系数法、等腰三角形的性质、二次函数的性质及转化思想等知识.在(1)中求得B、C的坐标是解题的关键,在(2)用P点坐标表示出PR和QR和长是解题的关键,在(3)①中把PR+QR转化成QM是解题的关键,在②中把△PQR的面积用PR表示出来是解题的关键.本题考查知识点较多,综合性较强,难度较大.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案科目:初中数学 来源: 题型:填空题
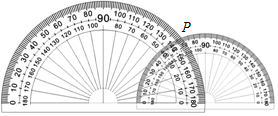 如图,小量角器的0°刻度线在大量角器的0°刻度线上,且小量角器的中心在大量角器的外缘边上.如果它们外缘边上的公共点P在大量角器上对应的度数为40°,那么在小量角器上对应的度数为70°.(只考虑小于90°的角度)
如图,小量角器的0°刻度线在大量角器的0°刻度线上,且小量角器的中心在大量角器的外缘边上.如果它们外缘边上的公共点P在大量角器上对应的度数为40°,那么在小量角器上对应的度数为70°.(只考虑小于90°的角度)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
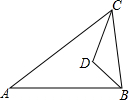 如图,在△ABC中,BD平分∠ABC,CD平分∠BCA,若∠D:∠A=7:2,则∠A的度数是( )
如图,在△ABC中,BD平分∠ABC,CD平分∠BCA,若∠D:∠A=7:2,则∠A的度数是( )| A. | 30° | B. | 32° | C. | 36° | D. | 40° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
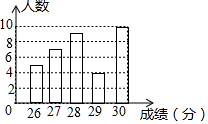 如图是某校910班参加2017年4月初中升学体育考试成绩(满分30分)的统计图,则该班这次体育升学考试成绩的中位数,众数分别是( )
如图是某校910班参加2017年4月初中升学体育考试成绩(满分30分)的统计图,则该班这次体育升学考试成绩的中位数,众数分别是( )| A. | 28分,30分 | B. | 28.5分,30分 | C. | 27.5分,28分 | D. | 28.2分,30分 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-2,-3) | B. | (2,3) | C. | (2,-3) | D. | (3,2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com