
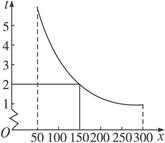
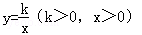 上的两点,BC∥x轴,交y轴于C,动点P从坐标原点O出发,沿O→A→B→C匀速运动,终点为C,过运动路线上任意一点P作PM⊥x轴于M,PN⊥y轴于N,设四边形OMPN的面积为S,P点运动的时间为t,则S关于t的函数图象大致是( )
上的两点,BC∥x轴,交y轴于C,动点P从坐标原点O出发,沿O→A→B→C匀速运动,终点为C,过运动路线上任意一点P作PM⊥x轴于M,PN⊥y轴于N,设四边形OMPN的面积为S,P点运动的时间为t,则S关于t的函数图象大致是( )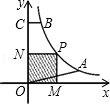
 B
B C
C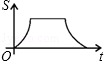 D
D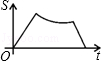
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:不详 题型:填空题
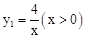 的图象上.反比例函数
的图象上.反比例函数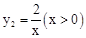 的图象经过点C,交AB于点D,则点D的坐标是 .
的图象经过点C,交AB于点D,则点D的坐标是 .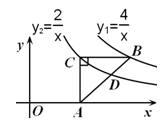
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
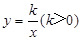 在第一象限图象上的一点,已知△P1O A1为等边三角形,点A1的坐标为(2,0).
在第一象限图象上的一点,已知△P1O A1为等边三角形,点A1的坐标为(2,0).
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 落在反比例函数
落在反比例函数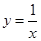 的图像上,另“7”字形有两个顶点落在
的图像上,另“7”字形有两个顶点落在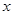 轴上,一个顶点落在
轴上,一个顶点落在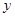 轴上.
轴上.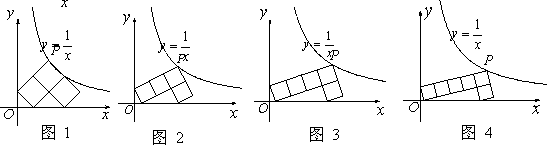
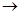 图2
图2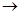 图3
图3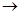 图4
图4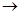
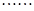 这样的规律拼接下去,第
这样的规律拼接下去,第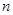 个图形中每一个小正方形的面积是 .(用含
个图形中每一个小正方形的面积是 .(用含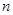 的代数式表示)
的代数式表示)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com