
【题目】如图,在△ABC中,AD和BE是高,∠ABE=45°,点F是AB的中点,AD与FE,BE分别交于点G、H.有下列结论:①FD=FE;②AH=2CD;③BCAD=![]() AE2;④S△ABC=2S△ADF.其中正确结论的序号是_____.(把你认为正确结论的序号都填上)
AE2;④S△ABC=2S△ADF.其中正确结论的序号是_____.(把你认为正确结论的序号都填上)

【答案】①②③
【解析】分析:仔细审题,首先根据直角三角形斜边上的中线性质得出FD=![]() AB,再证明△ABE是等腰直角三角形,进而可得FE=
AB,再证明△ABE是等腰直角三角形,进而可得FE=![]() AB,据此不难判断①是否正确;
AB,据此不难判断①是否正确;
根据已有信息易得∠ABC=∠C,进而可得出AB=AC,由等腰三角形的性质得出BC=2CD,∠BAD=∠CAD=∠CBE,由ASA证明△AEH≌△BEC,再结合全等三角形的性质判断②是否正确;
对于③,可通过证明△ABD~△BCE,得出BC:AB=BE:AD,即BC·AD=AB·BE,再由等腰直角三角形的性质和三角形的面积得出结论;
对于④,由F是AB的中点,BD=CD进行判断即可.
详解:∵在△ABC中,AD和BE是高,
∴∠ADB=∠AEB=∠CEB=90°,
∵点F是AB的中点,
∴FD=![]() AB,
AB,
∵∠ABE=45°,
∴△ABE是等腰直角三角形,
∴AE=BE,
∵点F是AB的中点,
∴FE=![]() AB,
AB,
∴FD=FE,①正确;
∵∠CBE=∠BAD,∠CBE+∠C=90°,∠BAD+∠ABC=90°,
∴∠ABC=∠C,
∴AB=AC,
∵AD⊥BC,
∴BC=2CD,∠BAD=∠CAD=∠CBE,
在△AEH和△BEC中,
∵∠AEH=∠CEB,
AE=BE,
∠EAH=∠CBE,
∴△AEH≌△BEC(ASA),
∴AH=BC=2CD,②正确;
∵∠BAD=∠CBE,∠ADB=∠CEB,
∴△ABD~△BCE,
∴![]() ,即BC·AD=AB·BE,
,即BC·AD=AB·BE,
∵![]() AE2=AB·AE=AB·BE,BC·AD=AC·BE=AB·BE,
AE2=AB·AE=AB·BE,BC·AD=AC·BE=AB·BE,
∴BC·AD=![]() AE2;③正确;
AE2;③正确;
∵F是AB的中点,BD=CD,∴
S△ABC=2S△ABD=4S△ADF.④错误;
故答案为:①②③.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CBF=![]() ∠CAB.
∠CAB.
(1)求证:直线BF是⊙O的切线;
(2)若AB=5,sin∠CBF=![]() ,求BC和BF的长.
,求BC和BF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:正方形ABCD和等腰直角三角形AEF,AE=AF(AE<AD),连接DE、BF,P是DE的中点,连接AP。将△AEF绕点A逆时针旋转。
(1)如图①,当△AEF的顶点E、F恰好分别落在边AB、AD时,则线段AP与线段BF的位置关系为 ,数量关系为 。
(2)当△AEF绕点A逆时针旋转到如图②所示位置时,证明:第(1)问中的结论仍然成立。
(3)若AB=3,AE=1,则线段AP的取值范围为 。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AD∥BC,对角线 AC、BD交于点 M,点E在边BC上,且∠DAE=∠DCB,联结AE,AE与BD交于点F.

(1)求证:![]() ;
;
(2)连接DE,如果BF=3FM,求证:四边形ABED是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1) (-3)+(-8)-(-6)-7;
(2)-30×(![]() -
-![]() +
+![]() );
);
(3) (![]() -
-![]() )÷(-
)÷(-![]() )2-23;
)2-23;
(4)-42÷![]() -0.25×[5-(-3)2].
-0.25×[5-(-3)2].
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=﹣x+4的图象与反比例函数y=![]() (k为常数,且k≠0)的图象交于A(1,a),B两点.
(k为常数,且k≠0)的图象交于A(1,a),B两点.
(1)求反比例函数的表达式及点B的坐标;
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标及△PAB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,AB=4![]() ,F是线段AC上一点,过点A的⊙F交AB于点D,E是线段BC上一点,且ED=EB,则EF的最小值为 ( )
,F是线段AC上一点,过点A的⊙F交AB于点D,E是线段BC上一点,且ED=EB,则EF的最小值为 ( )

A. 3![]() B. 2
B. 2![]() C.
C. ![]() D. 2
D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
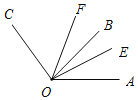
【题目】如图,OB为∠AOC内一条射线,∠AOB的余角是它自身的两倍.
(1)求∠AOB的度数;
(2)射线OE从OA开始,在∠AOB内以1°/s的速度绕着O点逆时针方向旋转,转到OB停止,同时射线OF在∠BOC内从OB开始以3°/s的速度绕O点逆时针方向旋转转到OC停止,设运动时间为t秒.
①若OE,OF运动的任一时刻,均有∠COF=3∠BOE,求∠AOC的度数;
②OP为∠AOC内任一射线,在①的条件下,当t=10时,以OP为边所有角的度数和的最小值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com