
【题目】如图,直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于
轴交于![]() 两点,与直线
两点,与直线![]() 交于点
交于点![]() .
.
(1)点![]() 坐标为( , ),B为( , ).
坐标为( , ),B为( , ).
(2)在线段![]() 上有一点
上有一点![]() ,过点
,过点![]() 作
作![]() 轴的平行线交直线
轴的平行线交直线![]() 于点
于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,若四边形
,若四边形![]() 是平行四边形时,求出此时
是平行四边形时,求出此时![]() 的值.
的值.
(3)若点![]() 为
为![]() 轴正半轴上一点,且
轴正半轴上一点,且![]() ,则在轴上是否存在一点
,则在轴上是否存在一点![]() ,使得
,使得![]() 四个点能构成一个梯形若存在,求出所有符合条件的
四个点能构成一个梯形若存在,求出所有符合条件的![]() 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.

【答案】(1)![]() 点的坐标是
点的坐标是![]() ,
,![]() 点的坐标是
点的坐标是![]() ;(2)
;(2)![]() ;(3)符合条件的
;(3)符合条件的![]() 点坐标为
点坐标为![]()
【解析】
(1)先将点C坐标代入直线l1中,求出直线l1的解析式,令x=0和y=0,即可得出结论;
(2)先求出直线l2的解析式,表示出点E,F的坐标,在判断出OB=EF,建立方程求解,即可得出结论;
(3)先求出点P的坐标,分两种情况求出直线PQ,AQ的解析式,即可得出结论.
解:(1)∵点C(2,![]() )在直线l1:
)在直线l1:![]() 上,
上,
∴![]() ,
,
∴直线l1的解析式为![]() ,
,
令x=0,∴y=3,∴B(0,3),
令y=0,∴![]() ,∴x=4,∴A(4,0),
,∴x=4,∴A(4,0),
故答案为:![]() 点的坐标是
点的坐标是![]() ,
,![]() 点的坐标是
点的坐标是![]() .
.
(2)∵![]() 轴,点
轴,点![]() 的横坐标为
的横坐标为![]() ,∴点
,∴点![]() 的横坐标也为
的横坐标也为![]() ,
,
∵直线![]() 与直线
与直线![]() 交于点
交于点![]()
∵点![]() 是直线
是直线![]() 的一点,
的一点,
∴点E的坐标是![]() ,
,
∵点![]() 是直线
是直线![]() 上的一点,
上的一点,
∴点![]() 的坐标是
的坐标是![]()
∵![]() 当
当![]()
![]()
![]()
(3)若点![]() 为
为![]() 轴正半轴上一点,
轴正半轴上一点,![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
![]()
当![]() 时
时
直线AB的解析式为:![]()
直线PQ的解析式为![]()
∴点![]() 的坐标是
的坐标是![]()
当![]() 时
时
直线BP的解析式为![]() ,
,
直线AQ的解析式为![]()
∴点![]() 的坐标是
的坐标是![]()
综上,在平面直角坐标系中存在点![]() ,使得
,使得![]() 四个点能构成一个梯形,符合条件的
四个点能构成一个梯形,符合条件的![]() 点坐标为
点坐标为![]()


科目:初中数学 来源: 题型:
【题目】如图,过点A(2,0)的两条直线![]() ,
,![]() 分别交
分别交![]() 轴于B,C,其中点B在原点上方,点C在原点下方,已知AB=
轴于B,C,其中点B在原点上方,点C在原点下方,已知AB=![]() .
.

(1)求点B的坐标;
(2)若△ABC的面积为4,求![]() 的解析式.
的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,矩形ABCD的顶点A、B分别在OM、ON上,当B在边ON上运动时,A 随之在边OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,则运动过程中,点C到点O的最大距离为___________.
,矩形ABCD的顶点A、B分别在OM、ON上,当B在边ON上运动时,A 随之在边OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,则运动过程中,点C到点O的最大距离为___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为鼓励节约用水,某地推行阶梯式水价计费制,标准如下:每月用水不超过17立方米的按每立方米![]() 元计费,超过17立方米而未超过30立方米的部分按每立方米
元计费,超过17立方米而未超过30立方米的部分按每立方米![]() 元计费,超过30立方米的部分按每立方米
元计费,超过30立方米的部分按每立方米![]() 元计费,某户居民上月用水35立方米,应缴水费_________元.
元计费,某户居民上月用水35立方米,应缴水费_________元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形A1A2A3A4,A5A6A7A8,A9A10A11A12,…(每个正方形从第三象限的顶点开始,按顺时针方向顺序,依次记为A1,A2,A3,A4;A5,A6,A7,A8;A9,A10,A11,A12;…)的中心均在坐标原点O,各边均与x轴或y轴平行,若它们的边长依次是2,4,6,…,则顶点A20的坐标为 ( )
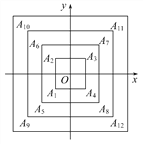
A. (5,5) B. (5,-5) C. (-5,5) D. (-5,-5)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】光明中学组织全校1000名学生进行了校园安全知识竞赛.为了解本次知识竞赛的成绩分布情况,从中随机抽取了部分学生的成绩(得分取正整数,满分为100分),并绘制了如图的频数分布表和频数分布直方图(不完整).
分组 | 频数 | 频率 |
50.5~60.5 | 10 | a |
60.5~70.5 | b | |
70.5~80.5 | 0.2 | |
80.5~90.5 | 52 | 0.26 |
90.5~100.5 | 0.37 | |
合计 | c | 1 |

请根据以上提供的信息,解答下列问题:
(1)直接写出频数分布表中a,b,c的值,补全频数分布直方图.
(2)上述学生成绩的中位数落在哪一组范围内?
(3)学校将对成绩在90.5~100.5分之间的学生进行奖励,请估计全校1000名学生中约有多少名获奖?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2011贵州安顺,9,3分)正方形ABCD边长为1,E、F、G、H分别为边AB、BC、CD、DA上的点,且AE=BF=CG=DH.设小正方形EFGH的面积为y,AE=x. 则y关于x的函数图象大致是( )

A. B. C. D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学问题:计算等差数列5,2,﹣1,﹣4……前n项的和.
问题探究:为解决上面的问题,我们从最简单的问题进行探究.
探究一:首先我们来认识什么是等差数列.
数学上,称按一定顺序排列的一列数为数列,其中排在第一位的数称为第1项,用a1表示:排在第二位的数称为第2项,用a2表示……排在第n位的数称为第n项,用an表示.一般地,如果一个数列从第二项起,每一项与它的前一项的差都等于同一个常数,那么这个数列叫做等差数列,这个常数叫等差数列的公差,公差通常用字母d表示.如:数列2,4,6,8,….为等差数列,其中a1=2,公差d=2.
(1)已知等差数列5,2,﹣1,﹣4,…则这个数列的公差d= ,第5项是 .
(2)如果一个数列a1,a2,a3,a4,…是等差数列,且公差为d,那么根据定义可得到:
a2﹣a1=d,a3﹣a2=d,a4﹣a3=d,……an﹣an﹣1=d,所以a2=a1+d,a3=a2+d=a1+2d,a4=a1+3d,……:由此可得an= (用a1和d的代数式表示)
(3)对于等差数列5,2,﹣1,﹣4,…,an= 请判断﹣2020是否是此等差数列的某一项,若是,请求出是第几项:若不是,说明理由.
探究二:二百多年前,数学王子高斯用他独特的方法快速计算出1+2+3+4+…+100的值.我们从这个算法中受到启发,用此方法计算数列1,2,3,…,n的前n项和:由 可知
可知![]()
(4)请你仿照上面的探究方式,解决下面的问题:
若a1,a2,a3,…,an为等差数列的前n项,前n项和Sn=a1+a2+a3+…+an.证明:Sn=na1+![]() .
.
(5)计算:计算等差数列5,2,﹣1,﹣4…前n项的和Sn(写出计算过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校准备印刷一批证书,现有两个印刷厂可供选择:甲厂收费方式:收制版费1000元,每本印刷费0.5元;乙厂收费方式:不收制版费,每本收印刷费1.5元;若该校印制证书x本.
(1)当印制证书3000本时,甲厂的收费为 元,乙厂的收费为 元;
(2)请问印刷多少本证书时,甲乙两厂收费相同?
(3)你认为选择哪一家印刷厂更优惠?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com