
分析 (1)首先根据P是线段OC上的动点,OP=m,设点P的坐标是(m,0),再根据∠PAD=90°,可得PA⊥AD,据此求出点P的坐标是多少;然后根据D在直线y=$\frac{3}{2}$x+6上,且AD=PA,求出点D的坐标是多少即可.
(2)首先求出点C关于OB对称点C′的坐标是多少;然后判断出当点C′、M、P在同一条直线上时,MP+MC取到最小值,且等于C′P,据此求出MP+MC的最小值是多少即可.
(3)直线y=$\frac{3}{2}$x+6向右平移6个单位后,在该直线上,存在点D(6,6),使△APD是等腰直角三角形,且∠PDA=90°.首先求出直线y=$\frac{3}{2}$x+6向右平移6个单位后的解析式是y=$\frac{3}{2}$x-3;然后求出直线y=$\frac{3}{2}$x-3与直线AB的交点是(6,6),即可判断出存在点D(6,6),使△APD是等腰直角三角形,且∠PDA=90°,此时点P的坐标是(6,0).
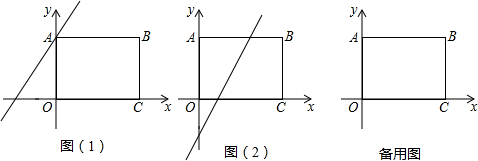
解答 解:(1)如图(1), ,
,
∵P是线段OC上的动点,OP=m,
∴设点P的坐标是(m,0),
∵∠PAD=90°,
∴PA⊥AD,
∵AD所在的直线的斜率是$\frac{3}{2}$,
∴PA所在的直线的斜率是-$\frac{2}{3}$,
∵四边形ABCO为矩形,且B的坐标为(9,6),
∴点A的坐标为(0,6),点C的坐标为(9,0),
∴$\frac{6}{-m}$=-$\frac{2}{3}$,
解得m=9,
∴点P的坐标为(9,0),点P和点C重合,
∴PA=$\sqrt{{6}^{2}{+9}^{2}}$=3$\sqrt{13}$,
又∵△APD等腰直角三角形,
∴AD=PA=3$\sqrt{13}$,
∵D在直线y=$\frac{3}{2}$x+6上,
∴设点D的坐标为(n,$\frac{3}{2}$n+6),
∴$\sqrt{{n}^{2}{+(\frac{3}{2}n+6-6)}^{2}}$=3$\sqrt{13}$,
解得n=6或n=-6,
∵点D在第三象限,
∴n=-6,
∴点D的坐标是(-6,-3).
(2)如图(2),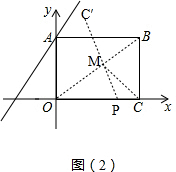 ,
,
∵B的坐标为(9,6),
∴OB所在的直线的解析式是y=$\frac{2}{3}$x,
设点C关于OB对称点C′的坐标是(c,d),
则$\left\{\begin{array}{l}{\frac{d}{c-9}×\frac{2}{3}=-1}\\{\frac{d}{2}=\frac{2}{3}×\frac{c+9}{2}}\end{array}\right.$
解得$\left\{\begin{array}{l}{c=\frac{45}{13}}\\{d=\frac{108}{13}}\end{array}\right.$
∴点C′的坐标是($\frac{45}{13}$,$\frac{108}{13}$),
∵点C关于OB对称点是C′,
∴MC′=MC,
∴当点C′、M、P在同一条直线上时,MP+MC取到最小值,且等于C′P,
∵m=$\frac{13}{2}$,
∴点P的坐标是($\frac{13}{2}$,0),
∴C′P=$\sqrt{{(\frac{45}{13}-\frac{13}{2})}^{2}{+(\frac{108}{13})}^{2}}$=$\frac{\sqrt{313}}{2}$,
∴MP+MC的最小值是$\frac{\sqrt{313}}{2}$.
(3)直线y=$\frac{3}{2}$x+6向右平移6个单位后,在该直线上,存在点D(6,6),使△APD是等腰直角三角形,且∠PDA=90°.
如图(3),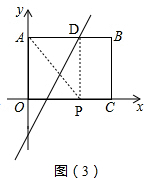 ,
,
直线y=$\frac{3}{2}$x+6向右平移6个单位后的解析式是:
y=$\frac{3}{2}$(x-6)+6=$\frac{3}{2}$x-3,
联立$\left\{\begin{array}{l}{y=\frac{3}{2}x-3}\\{y=6}\end{array}\right.$
解得$\left\{\begin{array}{l}{x=6}\\{y=6}\end{array}\right.$
∴直线y=$\frac{3}{2}$x-3与直线AB的交点是(6,6),
∴直线y=$\frac{3}{2}$x+6向右平移6个单位后,在该直线上,存在点D(6,6),使△APD是等腰直角三角形,且∠PDA=90°,此时点P的坐标是(6,0).
点评 (1)此题主要考查了一次函数综合题,考查了分析推理能力,考查了数形结合思想的应用,考查了从已知函数图象中获取信息,并能利用获取的信息解答相应的问题的能力.
(2)此题还考查了等腰直角三角形的性质和应用,要熟练掌握,解答此题的关键是要明确:等腰直角三角形是一种特殊的三角形,具有所有三角形的性质,还具备等腰三角形和直角三角形的所有性质.即:两个锐角都是45°,斜边上中线、角平分线、斜边上的高,三线合一,等腰直角三角形斜边上的高为外接圆的半径R,而高又为内切圆的直径.
(3)此题还考查了直线的平移,以及最值的求法,要熟练掌握.


科目:初中数学 来源: 题型:解答题
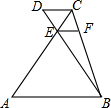 如图,AB∥CD∥EF,AC与BD相交于点E.
如图,AB∥CD∥EF,AC与BD相交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
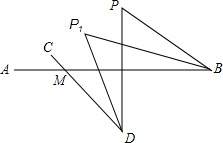 如图,BP1平分∠ABP,DP1平分∠CDP,将直线CD绕点D按顺时针方向旋转一定角度交直线AB于点M,判断∠P,∠P1,∠BMD的数量关系,并证明.
如图,BP1平分∠ABP,DP1平分∠CDP,将直线CD绕点D按顺时针方向旋转一定角度交直线AB于点M,判断∠P,∠P1,∠BMD的数量关系,并证明.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 在一次大型演出中,由1200名演员排出如图所示的正五边形队,内圈每边3人,往外每圈每边增加2人(即由内向外算起,第2圈每边5人,第三圈每边7人…),这样1200人恰好排完,则这个队共排了15圈.
在一次大型演出中,由1200名演员排出如图所示的正五边形队,内圈每边3人,往外每圈每边增加2人(即由内向外算起,第2圈每边5人,第三圈每边7人…),这样1200人恰好排完,则这个队共排了15圈.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
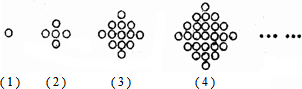
| A. | 145个 | B. | 162 | C. | 181个 | D. | 202个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com