
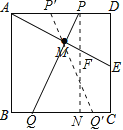
【题目】如图,正方形ABCD的边长为3cm,E为CD边上一点,∠DAE=30°,M为AE的中点,过点M作直线分别与AD、BC相交于点P、Q.若PQ=AE,则AP等于 cm.

【答案】1或2.
【解析】试题分析:根据题意画出图形,过P作PN⊥BC,交BC于点N,
∵四边形ABCD为正方形,
∴AD=DC=PN,
在Rt△ADE中,∠DAE=30°,AD=3cm,
∴tan30°=![]() ,即DE=
,即DE=![]() cm,
cm,
根据勾股定理得:AE=![]() cm,
cm,
∵M为AE的中点,
∴AM=![]() cm;
cm;
在Rt△ADE和Rt△PNQ中,AD=PN,AE=PQ,
∴Rt△ADE≌Rt△PNQ(HL),
∴DE=NQ,∠DAE=∠NPQ=30°,
∵PN∥DC,
∴∠PFA=∠DEA=60°,
∴∠PMF=90°,即PM⊥AF,
在Rt△AMP中,∠MAP=30°,cos30°=![]() ,
,
∴AP=2cm;
由对称性得到AP′=DP=AD-AP=3-2=1cm,
综上,AP等于1cm或2cm.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
【题目】某校八年级640名学生在“计算机应用”培训前、后各参加了一次水平相同的测试,并以同一标准分成“不合格”、“合格”、“优秀”3个等级,为了解培训效果,用抽样调查的方式从中抽取32名学生的2次测试等级,并绘制成条形统计图:

(1)这32名学生经过培训,测试等级“不合格”的百分比比培训前减少了多少?
(2)估计该校八年级学生中,培训前、后等级为“合格”与“优秀”的学生各有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一次数学活动课上,小颖用 10 个棱长为 1 的正方体积木搭成一个几何体,然后她请小华用其 他棱长为 1 的正方体积木在旁边再搭一个几何体,使用小华所搭几何体恰好和小颖所搭几何体拼成一个 无空隙的大正方体(不改变小颖所搭几何体的形状).那么:按照小颖的要求搭几何体,小华至少需要_____个正方体积木.按照小颖的要求,小华所搭几何体的表面积最小为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点G、E、F分别在平行四边形ABCD的边AD、DC和BC上,DG=DC,CE=CF,点P是射线GC上一点,连接FP,EP,求证:FP=EP.
查看答案和解析>>
科目:初中数学 来源: 题型:
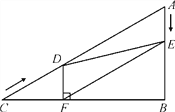
【题目】如图,在Rt△ABC中,∠B=90°,AC=60 cm,∠A=60°,点D从点C出发沿CA方向以4 cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2 cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D,E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF。
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,请说明理由;
(3)当t为何值时,△DEF为直角三角形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在坐标系中放置一菱形OABC,已知∠ABC=60°,OA=1.先将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2014次,点B的落点依次为B1,B2,B3,…,则B2014的坐标为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
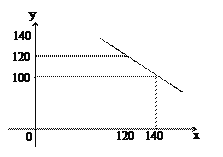
【题目】某商店试销一种成本单价为100元/件的运动服,规定试销时的销售单价不低于成本单价,又不高于180元/件,经市场调查,发现销售量y(件)与销售单价x(元)之间的关系满足一次函数y=kx+b(k≠0),其图象如图。
(1)根据图象,求一次函数的解析式;
(2)当销售单价x在什么范围内取值时,销售量y不低于80件。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知 ![]() ABC的三个顶点的坐标分别为A(-1,1), B(-3,1),C(-1,4).
ABC的三个顶点的坐标分别为A(-1,1), B(-3,1),C(-1,4).
①画出△ABC关于y轴对称的△A1B1C1;
②将△ABC绕着点B顺时针旋转90°后得到△A2BC2 , 请在图中画出△A2BC2 , 并求出线段BC旋转过程中所扫过的面积(结果保留 ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在解决数学问题的过程中,我们常用到“分类讨论”的数学思想,下面是运用分类讨论的数学思想解决问题的过程,请仔细阅读,并解答题目后提出的(探究).
(提出问题)两个有理数a、b满足a、b同号,求![]() 的值.
的值.
(解决问题)解:由a、b同号,可知a、b有两种可能:①当a,b都正数;②当a,b都是负数.①若a、b都是正数,即a>0,b>0,有|a|=a,|b|=b,则![]() =
=![]() =1+1=2;②若a、b都是负数,即a<0,b<0,有|a|=﹣a,|b|=﹣b,则
=1+1=2;②若a、b都是负数,即a<0,b<0,有|a|=﹣a,|b|=﹣b,则![]() =
=![]() =(﹣1)+(﹣1)=﹣2,所以
=(﹣1)+(﹣1)=﹣2,所以![]() 的值为2或﹣2.
的值为2或﹣2.
(探究)请根据上面的解题思路解答下面的问题:
(1)两个有理数a、b满足a、b异号,求![]() 的值;
的值;
(2)已知|a|=3,|b|=7,且a<b,求a+b的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com