
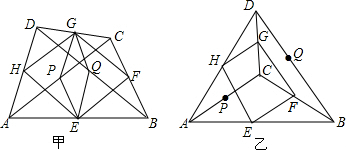
分析 (1)根据三角形的中位线定理,得GH∥EF∥AC,GH=EF=$\frac{1}{2}$AC,所以得到的是平行四边形;根据三角形的中位线定理,得GP∥EQ∥AD,GP=EQ=$\frac{1}{2}$AD,所以得到的是平行四边形.
(2)类似于(1)中的2个结论都成立:根据三角形的中位线定理,得GH∥EF∥AC,GH=EF=$\frac{1}{2}$AC,所以得到的是平行四边形;根据三角形的中位线定理,得GP∥EQ∥AD,GP=EQ=$\frac{1}{2}$AD,所以得到的是平行四边形.
解答  解:(1)四边形EFGH是平行四边形.理由如下:
解:(1)四边形EFGH是平行四边形.理由如下:
∵E、F分别是AB、BC的中点,
∴EF∥AC,EF=$\frac{1}{2}$AC.
同理,得HG∥AC,HG=$\frac{1}{2}$AC,
∴EF∥HG,EF=HG,
∴四边形EFGH是平行四边形.
四边形PEQG是平行四边形.理由如下:
∵G、P分别是CD、AC的中点,
∴GP∥AD,GP=$\frac{1}{2}$AD.
同理,得QE∥AD,QE=$\frac{1}{2}$AD,
∴GP∥QE,GP=QE,
∴四边形PEQG是平行四边形.
(2)(1)中的两个结论都成立.
四边形EFGH是平行四边形.理由如下:
∵E、F分别是AB、BC的中点,
∴EF∥AC,EF=$\frac{1}{2}$AC.
同理,得HG∥AC,HG=$\frac{1}{2}$AC,
∴EF∥HG,EF=HG,
∴四边形EFGH是平行四边形.
如图乙,顺次连接EQ,QG,GP,PE,得到四边形PEQG.
四边形PEQG是平行四边形.理由如下:
∵G、P分别是CD、AC的中点,
∴GP∥AD,GP=$\frac{1}{2}$AD.
同理,得QE∥AD,QE=$\frac{1}{2}$AD,
∴GP∥QE,GP=QE,
∴四边形PEQG是平行四边形.
点评 主要考查了平行四边形的判定和三角形的中位线定理.
数量关系:三角形的中位线等于第三边一半.位置关系:三角形中位线平行于第三边.
总结:顺次连接四边形各边中点所得四边形是平行四边形.


 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com