
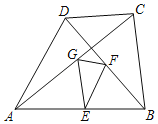
【题目】如图,如果四边形ABCD中,AD=BC=6,点E、F、G分别是AB、BD、AC的中点,那么△EGF面积的最大值为_____.
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象的顶点在第一象限,且过点(0,1)和(﹣1,0),下列结论:①ab<0,②b2﹣4ac>0,③a﹣b+c<0,④c=1,⑤当x>﹣1时,y>0.其中正确结论的个数是( )

A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践:活动课上,某数学兴趣小组在操场看到马路上行驶的汽车,突发奇想:“想测量汽车的速度”.他们想到的方法是:如图,一人站在![]() 长且平行于公路(
长且平行于公路(![]() )的巨型广告牌(
)的巨型广告牌(![]() )前的点
)前的点![]() 处.广告牌恰好挡住了此人的视线,将看不到的那段公路记为
处.广告牌恰好挡住了此人的视线,将看不到的那段公路记为![]() .已知此人到广告牌和广告牌到公路的距离分别是
.已知此人到广告牌和广告牌到公路的距离分别是![]() 和
和![]() ,一辆匀速行驶的汽车经过公路
,一辆匀速行驶的汽车经过公路![]() 段的时间是
段的时间是![]() (不计汽车长度),请作答:
(不计汽车长度),请作答:

(1)请在图上画出线段![]() ;
;
(2)求该汽车的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
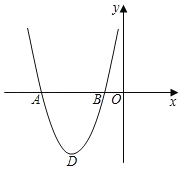
【题目】如图,在平面直角坐标系中,抛物线C1经过点A(﹣4,0)、B(﹣1,0),其顶点为![]() .
.
(1)求抛物线C1的表达式;
(2)将抛物线C1绕点B旋转180°,得到抛物线C2,求抛物线C2的表达式;
(3)再将抛物线C2沿x轴向右平移得到抛物线C3,设抛物线C3与x轴分别交于点E、F(E在F左侧),顶点为G,连接AG、DF、AD、GF,若四边形ADFG为矩形,求点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象顶点坐标为(1,4),且经过点C(3,0).
(1)求该二次函数的解析式;
(2)当x取何值时,y随x的增大而减小?
(3)当![]() 时,直接写出x的取值范围.
时,直接写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线与x轴相交于A、B两点,与y轴的交于点C,其中A点的坐标为(﹣3,0),点C的坐标为(0,﹣3),对称轴为直线x=﹣1.
(1)求抛物线的解析式;
(2)若点P在抛物线上,且S△POC=4S△BOC,求点P的坐标;
(3)设点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
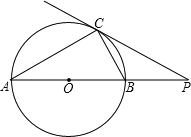
【题目】如图,点P在⊙O外,PC是⊙O的切线,C为切点,直线PO与⊙O相交于点A、B.
(1)若∠A=30°,求证:PA=3PB;
(2)小明发现,∠A在一定范围内变化时,始终有∠BCP=![]() (90°﹣∠P)成立.请你写出推理过程.
(90°﹣∠P)成立.请你写出推理过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:①abc<0;②4ac<b2;③方程ax2+bx+c=0的两个根是x1=﹣1,x2=3;④3a+c>0;⑤当y≥0时,x的取值范围是﹣1≤x≤3.其中结论正确的个数是( )
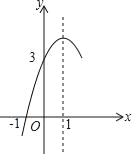
A. 1个B. 2个C. 3D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com