
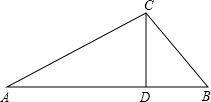
 (2012•包河区二模)如图,在一笔直的公路上有相距2000米的A、B两点,此时公路的正上方有一架飞机C,小明站在点A处,看飞机C,测得仰角为30°,小王在B处看飞机C,测得仰角为45°,求此时飞机的大约高度CD.(小明、小王的身高忽略不计,参考数据
(2012•包河区二模)如图,在一笔直的公路上有相距2000米的A、B两点,此时公路的正上方有一架飞机C,小明站在点A处,看飞机C,测得仰角为30°,小王在B处看飞机C,测得仰角为45°,求此时飞机的大约高度CD.(小明、小王的身高忽略不计,参考数据| 2 |
| 3 |
| 3 |
| CD |
| tan30° |
| 3 |
| 3 |
| 3 |


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
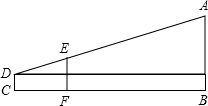 (2012•包河区二模)如图所示,在数学活动课上,几个同学用如下方法测量学校旗杆的高度:人站在距旗杆AB底部40米的C处望旗杆顶A,水平移动标杆EF,使C、F、B在同一直线上,D、E、A也在同一直线上,此时测得CF距离为2.5米,已知标杆EF长2.5米,人的视线高度CD为1.5米.则旗杆AB高为( )
(2012•包河区二模)如图所示,在数学活动课上,几个同学用如下方法测量学校旗杆的高度:人站在距旗杆AB底部40米的C处望旗杆顶A,水平移动标杆EF,使C、F、B在同一直线上,D、E、A也在同一直线上,此时测得CF距离为2.5米,已知标杆EF长2.5米,人的视线高度CD为1.5米.则旗杆AB高为( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com