
分析 (1)方程移项后,左边分解因式后,利用两数相乘积为0,两因式中至少有一个为0转化为两个一元一次方程来求解.
(2)方程左边分解因式后,利用两数相乘积为0,两因式中至少有一个为0转化为两个一元一次方程来求解.
解答 解:(1)2(x-3)=3x(x-3).
(x-3)(3x-2)=0,
∴x-3=0或3x-2=0,
∴x1=3或x2=$\frac{2}{3}$.
(2)2x2-3x+1=0.
(x-1)(2x-1)=0,
∴x-1=0或2x-1=0,
∴x1=1或x2=$\frac{1}{2}$.
点评 本题考查了解一元二次方程-因式分解法:把一元二次方程变形为一般式,再把方程左边进行因式分解,然后把方程转化为两个一元一次方程,解这两个一元一次方程得到原方程的解.


科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ② | C. | ③ | D. | ②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 居民 | 1 | 2 | 3 | 4 |
| 月用电量(度/户) | 30 | 42 | 50 |
| A. | 中位数是50 | B. | 众数是51 | C. | 方差是42 | D. | 平均数为46.8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
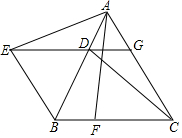 如图,△ABC是等边三角形,过AB边上的点D作GD∥BC,交AC于点G,在GD的延长线上取点E,使DE=DB,连接AE、CD;
如图,△ABC是等边三角形,过AB边上的点D作GD∥BC,交AC于点G,在GD的延长线上取点E,使DE=DB,连接AE、CD;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 日期 | 星期日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 |
| 吨数 | +11 | -12 | -16 | +35 | -23 | -20 | -15 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 数学综合实践活动课上,小明将等腰直角三角板放在两墙墩之间,如图所示.
数学综合实践活动课上,小明将等腰直角三角板放在两墙墩之间,如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com