
 如图,平面直角坐标系中,点A、B、C在x轴上,点D、E在y轴上,OA=OD=2,OC=OE=4,B为线段OA的中点,直线AD与经过B、E、C三点的抛物线交于F、G两点,与其对称轴交于M,点P为线段FG上一个动点(与F、G不重合),
如图,平面直角坐标系中,点A、B、C在x轴上,点D、E在y轴上,OA=OD=2,OC=OE=4,B为线段OA的中点,直线AD与经过B、E、C三点的抛物线交于F、G两点,与其对称轴交于M,点P为线段FG上一个动点(与F、G不重合),分析 (1)利用待定系数法即可求得二次函数的解析式;
(2)根据等腰三角形的定义,分OP=OC,PC=OC,OP=PC三种情况即可求得P的坐标;
(3)设点P为(x,x+2)Q(x,-x2+3x+4),则PQ=-x2+2x+2,根据PQNM是菱形,则PQ=MN,即可求得PM的长,判断是否成立,从而确定;根据全等三角形的判定与性质,可得NQ=MP,根据NH=MG,可得$\frac{25}{4}$-(-x2+3x+4)=x+2-$\frac{7}{2}$,根据解方程,可确定P的坐标.
解答 解:(1)∵B(-1,0)E(0,4)C(4,0)
设解析式是y=ax2+bx+c
可得 $\left\{\begin{array}{l}a-b+c=0\\ c=4\\ 16a+4b+c=0\end{array}\right.$解得$\left\{\begin{array}{l}a=-1\\ b=3\\ c=4\end{array}\right.$
∴y=-x2+3x+4;
(2)∵点A坐标是(-2,0),点D坐标是(0,2)
直线AD的解析式是y=x+2,
设点P坐标是(x,x+2),
当OP=OC时,x2+(x+2)2=16 解得$x=1±\sqrt{7}$($x=1-\sqrt{7}$不符合,舍去)此时点P($1+\sqrt{7},3+\sqrt{7}$),
当PC=OC时,(x+2)2+(4-x)2=16方程无解,
当PO=PC时,点P在OC的中垂线上,
∴点P横坐标是2,得点P坐标是(2,4),
∴当△POC是等腰三角形时,点P坐标是($1+\sqrt{7},3+\sqrt{7}$)或(2,4);
(3)点M坐标是($\frac{3}{2}$,$\frac{7}{2}$)N坐标是($\frac{3}{2},\frac{25}{4}$)
∴MN=$\frac{11}{4}$,
设点P 为(x,x+2)Q(x,-x2+3x+4),则PQ=-x2+2x+2,
①若PQNM是菱形,则PQ=MN,可得x1=0.5,x2=1.5.
当x2=1.5时,点P与点M重合;当x1=0.5时,可求得PM=$\sqrt{2}$,
所以菱形不存在.
②能成为等腰梯形,如图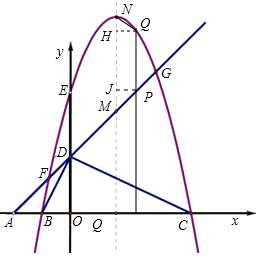 ,QH⊥MN于点H,作PJ⊥MN于点J,
,QH⊥MN于点H,作PJ⊥MN于点J,
△NHQ≌△MJP,
∴NQ=MP.
∴四边形NMPQ是等腰梯形.
由NH=MJ,
得$\frac{25}{4}$-(-x2+3x+4)=x+2-$\frac{7}{2}$,
解得:x=2.5,
此时点P的坐标是(2.5,4.5).
点评 本题是二次函数的综合题,解(1)的关键是待定系数法,解(2)的关键利用等腰三角形的定义得出关于x的方程,要分类讨论,以防遗漏;解(3)的关键是利用菱形的判定及等腰梯形的判定.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
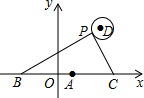 如图,在平面直角坐标系中,已知点A(1,0),B(1-a,0),C(1+a,0)(a>0),点P在以D(3,3)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则a的最大值是$\sqrt{13}+1$.
如图,在平面直角坐标系中,已知点A(1,0),B(1-a,0),C(1+a,0)(a>0),点P在以D(3,3)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则a的最大值是$\sqrt{13}+1$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
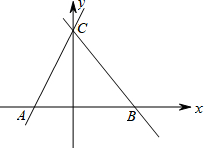 如图,直线y=-$\frac{4}{3}$x+4与x轴、y轴的交点分别为B,C,点A的坐标为(-2,0).
如图,直线y=-$\frac{4}{3}$x+4与x轴、y轴的交点分别为B,C,点A的坐标为(-2,0).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
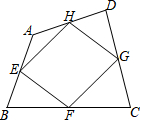 如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,若四边形EFGH为矩形,则四边形ABCD的对角线AC与BD须满足的关系为AC⊥BD.
如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,若四边形EFGH为矩形,则四边形ABCD的对角线AC与BD须满足的关系为AC⊥BD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
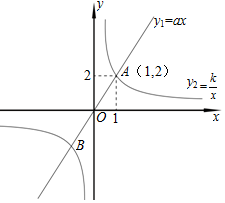 如图,已知正比例函数y1=ax的图象与反比例函数y2=$\frac{k}{x}$ 的图象有一个公共点A(1,2).
如图,已知正比例函数y1=ax的图象与反比例函数y2=$\frac{k}{x}$ 的图象有一个公共点A(1,2).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
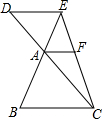 如图,若BC∥DE∥AF 则下列结论中:
如图,若BC∥DE∥AF 则下列结论中:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=1,将△ABC绕点C顺时针旋转得△A1B1C1,且点A1落在边AB边上,取BB1的中点D,连接CD,则CD的长为( )
如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=1,将△ABC绕点C顺时针旋转得△A1B1C1,且点A1落在边AB边上,取BB1的中点D,连接CD,则CD的长为( )| A. | $\frac{3}{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com