
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
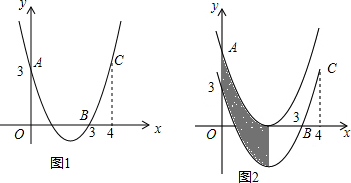
分析 把点A、B、C代入抛物线解析式y=ax2+bx+c利用待定系数法求解即可;把抛物线解析式整理成顶点式形式,然后写出顶点坐标;根据顶点坐标求出向上平移的距离,再根据阴影部分的面积等于平行四边形的面积,列式进行计算即可得解.
解答 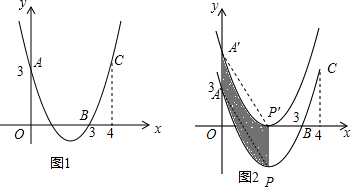 解:∵抛物线y=ax2+bx+c经过点A(0,3),B(3,0),C(4,3),
解:∵抛物线y=ax2+bx+c经过点A(0,3),B(3,0),C(4,3),
∴$\left\{\begin{array}{l}{c=3}\\{9a+3b+c=0}\\{16a+4b+c=3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=1}\\{b=-4}\\{c=3}\end{array}\right.$,
∴抛物线的函数表达式为y=x2-4x+3;
∴y=x2-4x+3=(x-2)2-1,
∴抛物线的顶点坐标为(2,-1),
∴PP′=1,
阴影部分的面积等于平行四边形A′APP′的面积,
平行四边形A′APP′的面积=1×2=2,
∴阴影部分的面积=2.
故选B.
点评 本题考查了待定系数法求二次函数解析式,二次函数的性质,二次函数图象与几何变换,根据平移的性质,把阴影部分的面积转化为平行四边形的面积是解题的关键.


科目:初中数学 来源: 题型:解答题
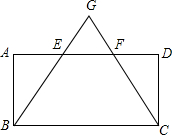 如图,在平行四边形ABCD中,E、F为AD上两点,AE=EF=FD,连接BE、CF并延长,交于点G,GB=GC.
如图,在平行四边形ABCD中,E、F为AD上两点,AE=EF=FD,连接BE、CF并延长,交于点G,GB=GC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
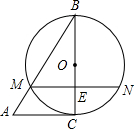 如图,在△ABC中,以BC为直径的⊙O交AB于M,弦MN∥AC且MN交BC于点E,ME=1,BM=2,BE=$\sqrt{3}$.
如图,在△ABC中,以BC为直径的⊙O交AB于M,弦MN∥AC且MN交BC于点E,ME=1,BM=2,BE=$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
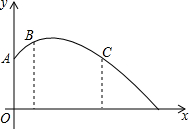 如图,一个圆形喷水池的中央垂直于水面安装了一个柱形喷水装置OA,O恰好在水面中心,安置在柱子顶端A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,且在过OA的任一平面上,按如图所示建立直角坐标系,水流喷出的高度y(m)与水平距离x(m)之间的关系式可以用y=-x2+bx+c表示,且抛物线经过点B($\frac{1}{2}$,$\frac{5}{2}$),C(2,$\frac{7}{4}$).
如图,一个圆形喷水池的中央垂直于水面安装了一个柱形喷水装置OA,O恰好在水面中心,安置在柱子顶端A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,且在过OA的任一平面上,按如图所示建立直角坐标系,水流喷出的高度y(m)与水平距离x(m)之间的关系式可以用y=-x2+bx+c表示,且抛物线经过点B($\frac{1}{2}$,$\frac{5}{2}$),C(2,$\frac{7}{4}$).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com