
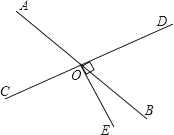
【题目】如图,AB和CD相交于点O,∠DOE=90°,若∠BOE=![]() ∠AOC,
∠AOC,
(1)指出与∠BOD相等的角,并说明理由.
(2)求∠BOD,∠AOD的度数.
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=70°,∠C=30°.求:
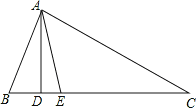
(1)∠BAE的度数;
(2)∠DAE的度数;
(3)探究:小明认为如果条件∠B=70°,∠C=30°改成∠B-∠C=40°,也能得出∠DAE的度数?若能,请你写出求解过程;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
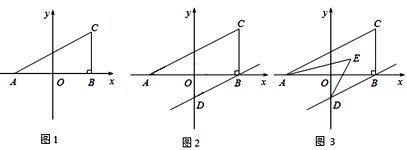
【题目】如图1,在平面直角坐标系中,A(a,0),C(b,2),且满足![]() ,过C作
,过C作![]() 轴于B,
轴于B,
(1)求a,b的值;
(2)在y轴上是否存在点P,使得△ABC和△OCP的面积相等,若存在,求出点P坐标,若不存在,试说明理由.
(3)若过B作BD∥AC交y轴于D,且AE,DE分别平分∠CAB,∠ODB,如图2,图3,
①求:∠CAB+∠ODB的度数;
②求:∠AED的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD平分∠BAC,DE∥AC交AB于E,DF∥AB交AC于F,若AF=6,则四边形AEDF的周长是( )

A. 24 B. 28 C. 32 D. 36
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面文字,根据所给信息解答下面问题:把几个数用大括号括起来,中间用逗号隔开,如:{3,4};{﹣3,6,8,18},其中大括号内的数称其为集合的元素.如果一个集合满足:只要其中有一个元素a,使得﹣2a+4也是这个集合的元素,这样的集合称为条件集合.例如;{3,﹣2},因为﹣2×3+4=﹣2,﹣2恰好是这个集合的元素所以吕{3,﹣2}是条件集合:例如;(﹣2,9,8,},因为﹣2×(﹣2)+4=8,8恰好是这个集合的元素,所以{﹣2,9,8,}是条件集合.
(1)集合{﹣4,12}是否是条件集合?
(2)集合{![]() ,﹣
,﹣![]() ,
,![]() }是否是条件集合?
}是否是条件集合?
(3)若集合{8,n}和{m}都是条件集合.求m、n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【操作发现】
如图①,在边长为1个单位长度的小正方形组成的网格中,△ABC的三个顶点均在格点上.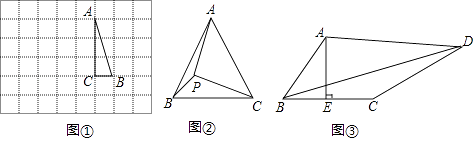
(1)请按要求画图:将△ABC绕点A按顺时针方向旋转90°,点B的对应点为B′,点C的对应点为C′,连接BB′;
(2)在(1)所画图形中,∠AB′B= .
(3)【问题解决】
如图②,在等边三角形ABC中,AC=7,点P在△ABC内,且∠APC=90°,∠BPC=120°,求△APC的面积.
小明同学通过观察、分析、思考,对上述问题形成了如下想法:
想法一:将△APC绕点A按顺时针方向旋转60°,得到△AP′B,连接PP′,寻找PA,PB,PC三条线段之间的数量关系;
想法二:将△APB绕点A按逆时针方向旋转60°,得到△AP′C′,连接PP′,寻找PA,PB,PC三条线段之间的数量关系.
…
请参考小明同学的想法,完成该问题的解答过程.(一种方法即可)
(4)【灵活运用】
如图③,在四边形ABCD中,AE⊥BC,垂足为E,∠BAE=∠ADC,BE=CE=2,CD=5,AD=kAB(k为常数),求BD的长(用含k的式子表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com