
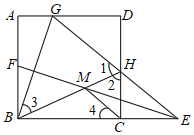
【题目】如图,正方形ABCD中,E是BC延长线上一点,在AB上取一点F,使点B关于直线EF的对称点G落在AD上,连接EG交CD于点H,连接BH交EF于点M,连接CM.则下列结论,其中正确的是( )
①∠1=∠2;
②∠3=∠4;
③GD=![]() CM;
CM;
④若AG=1,GD=2,则BM=![]() .
.
A.①②③④B.①②C.③④D.①②④
【答案】A
【解析】
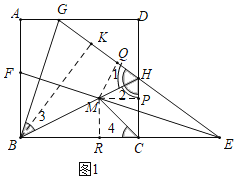
①正确.如图1中,过点B作BK⊥GH于K.想办法证明Rt△BHK≌Rt△BHC(HL)可得结论.
②正确.分别证明∠GBH=45°,∠4=45°即可解决问题.
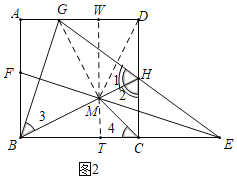
③正确.如图2中,过点M作MW⊥AD于W,交BC于T.首先证明MG=MD,再证明△BTM≌△MWG(AAS),推出MT=WG可得结论.
④正确.求出BT=2,TM=1,利用勾股定理即可判断.
解:如图1中,过点B作BK⊥GH于K.
∵B,G关于EF对称,
∴EB=EG,
∴∠EBG=∠EGB,
∵四边形ABCD是正方形,
∴AB=BC,∠A=∠ABC=∠BCD=90°,AD∥BC,
∴∠AGB=∠EBG,
∴∠AGB=∠BGK,
∵∠A=∠BKG=90°,BG=BG,
∴△BAG≌△BKG(AAS),
∴BK=BA=BC,∠ABG=∠KBG,
∵∠BKH=∠BCH=90°,BH=BH,
∴Rt△BHK≌Rt△BHC(HL),
∴∠1=∠2,∠HBK=∠HBC,故①正确,
∴∠GBH=∠GBK+∠HBK=![]() ∠ABC=45°,
∠ABC=45°,
过点M作MQ⊥GH于Q,MP⊥CD于P,MR⊥BC于R.
∵∠1=∠2,
∴MQ=MP,
∵∠MEQ=∠MER,
∴MQ=MR,
∴MP=MR,
∴∠4=∠MCP=![]() ∠BCD=45°,
∠BCD=45°,
∴∠GBH=∠4,故②正确,
如图2中,过点M作MW⊥AD于W,交BC于T.
∵B,G关于EF对称,
∴BM=MG,
∵CB=CD,∠4=∠MCD,CM=CM,
∴△MCB≌△MCD(SAS),
∴BM=DM,
∴MG=MD,
∵MW⊥DG,
∴WG=WD,
∵∠BTM=∠MWG=∠BMG=90°,
∴∠BMT+∠GMW=90°,
∵∠GMW+∠MGW=90°,
∴∠BMT=∠MGW,
∵MB=MG,
∴△BTM≌△MWG(AAS),
∴MT=WG,
∵MC=![]() TM,DG=2WG,
TM,DG=2WG,
∴DG=![]() CM,故③正确,
CM,故③正确,
∵AG=1,DG=2,
∴AD=AB=TM=3,EM=WD=TM=1,BT=AW=2,
∴BM=![]() ,故④正确,
,故④正确,
故选:A.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】为了节能减排,我市某校准备购买某种品牌的节能灯,已知3只A型节能灯和5只B型节能灯共需50元,2只A型节能灯和3只B型节能灯共需31元.
(1)求1只A型节能灯和1只B型节能灯的售价各是多少元?
(2)学校准备购买这两种型号的节能灯共200只,要求A型节能灯的数量不超过B型节能灯的数量的3倍,请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC与△CDE中,∠ACB![]() ∠CDE
∠CDE![]() 90°,AC
90°,AC![]() BC,CD
BC,CD![]() ED,连接AE,BE,F为AE的中点,连接DF,△CDE绕着点C旋转.
ED,连接AE,BE,F为AE的中点,连接DF,△CDE绕着点C旋转.
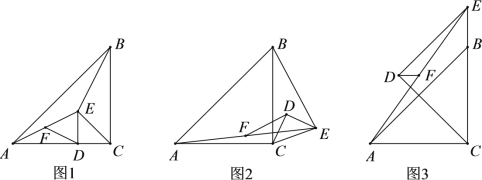
(1)如图1,当点D落在AC上时,DF与BE的数量关系是: ;
(2)如图2,当△CDE旋转到该位置时,DF与BE是否仍具有(1)中的数量关系,如果具有,请给予证明;如果没有,请说明理由;
(3)如图3,当点E落在线段CB延长线上时,若CD![]() AC
AC![]() 2,求DF的长.
2,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解,并解答问题:
如图所示的8×8网格都是由边长为1的小正方形组成,图①中的图案是3世纪我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”.赵爽通过对这种图形切割、拼接,巧妙地利用面积关系证明了著名的勾股定理,它表现了我国古人对数学的钻研精神和聪明才智,是我国数学史上的骄傲.

问题:
请用“赵爽弦图”中的四个直角三角形通过你所学过的图形变化,在图②,图③的方格纸中设计另外两个不同的图案,每个直角三角形的顶点均在方格纸的格点上,且四个三角形互不重叠.画图要求:
(1)图②中所设计的图案(不含方格纸)必须是轴对称图形但不是中心对称图形;
(2)图③中所设计的图案(不含方格纸)必须既是轴对称图形,又是中心对称图形.
查看答案和解析>>
科目:初中数学 来源: 题型:
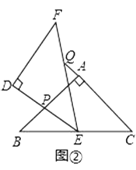
【题目】△ABC和△DEF是两个全等的等腰直角三角形,∠BAC=∠EDF=90°,△EDF的顶点E与△ABC的斜边BC的中点重合,将△DEF绕点E旋转,旋转过程中,线段DE与线段AB相交于点P,线段EF与射线CA相交于点Q.
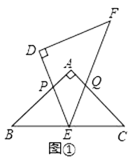
(1)如图①,当点Q在线段AC上,且AP=AQ时,求证:△BPE≌△CQE;
(2)如图②,当点Q在线段CA的延长线上时,求证:△BPE∽△CEQ;
(3)在(2)的条件下,BP=2,CQ=9,则BC的长为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】因“抗击疫情”需要,学校决定再次购进一批医用一次性口罩及KN95口罩共1000只,已知1只医用一次性口罩和10只KN95口罩共需113元;3只医用一次性口罩和5只KN95口罩共需64元.问:
(1)一只医用一次性口罩和一只KN95口罩的售价分别是多少元?
(2)参照上次购买获得的需求情况后,校长给出了一条建议:医用一次性口罩的购买量不能多于KN95口罩数量的2倍,请你遵循校长建议给出最省钱的购买方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小林家的洗手台面上有一瓶洗手液(如图1),当手按住顶部A下压时(如图2),洗手液瞬间从喷口B流出,已知瓶子上部分的![]() 和
和![]() 的圆心分别为D,C,下部分的视图是矩形CGHD,GH=10cm,GC=8cm,点E到台面GH的距离为14cm,点B距台面GH的距离为16cm,且B,D,H三点共线.如果从喷口B流出的洗手液路线呈抛物线形,且该路线所在的抛物线经过C.E两点,接洗手液时,当手心O距DH的水平距离为2cm时,手心O距水平台面GH的高度为_____cm.
的圆心分别为D,C,下部分的视图是矩形CGHD,GH=10cm,GC=8cm,点E到台面GH的距离为14cm,点B距台面GH的距离为16cm,且B,D,H三点共线.如果从喷口B流出的洗手液路线呈抛物线形,且该路线所在的抛物线经过C.E两点,接洗手液时,当手心O距DH的水平距离为2cm时,手心O距水平台面GH的高度为_____cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
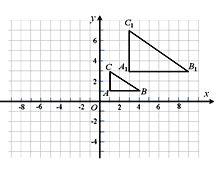
【题目】如图,在平面直角坐标系中,将△ABC进行位似变换得到△A1B1C1.
(1)△ABC与△A1B1C1的位似比是 .
(2)画出△ABC绕点O逆时针旋转180°得到的△A2B2C2.
(3)若点P(a,b)为△ABC内一点,求点P在△A2B2C2内的对应点P2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某地有甲、乙两栋建筑物,小明于乙楼楼顶A点处看甲楼楼底D点处的俯角为45°,走到乙楼B点处看甲楼楼顶E点处的俯角为60°,已知AB=6m,DE=10m.求乙楼的高度AC的长.(参考数据:![]() ,
,![]() ,精确到0.1m.)
,精确到0.1m.)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com